- 公開日:
ヒストグラムとは?エクセルによるヒストグラムの作り方(書き方)
レポートやプレゼンなどでデータを視覚化するとわかりやすくなります。データのばらつきをグラフとして表したいときに便利なのがヒストグラムです。
Excel 2016以降を使えば簡単にヒストグラムを作成できます。ヒストグラムの意味から作成方法、見方まで幅広く解説しています。
ヒストグラムとは?
ヒストグラムについて意味や例、特徴などを説明します。
ヒストグラムの意味
ヒストグラム(histogram)とは、度数分布表をグラフにしたものです。度数分布表とは、データをいくつかの区間(階級)に分け、それぞれの区間に含まれるデータの個数(度数)を表の形式で表したものです。
度数分布図、柱状グラフとも呼ばれます。品質管理の手法(フレームワーク)である「QC七つ道具」の1つです。
ヒストグラムの横軸と縦軸
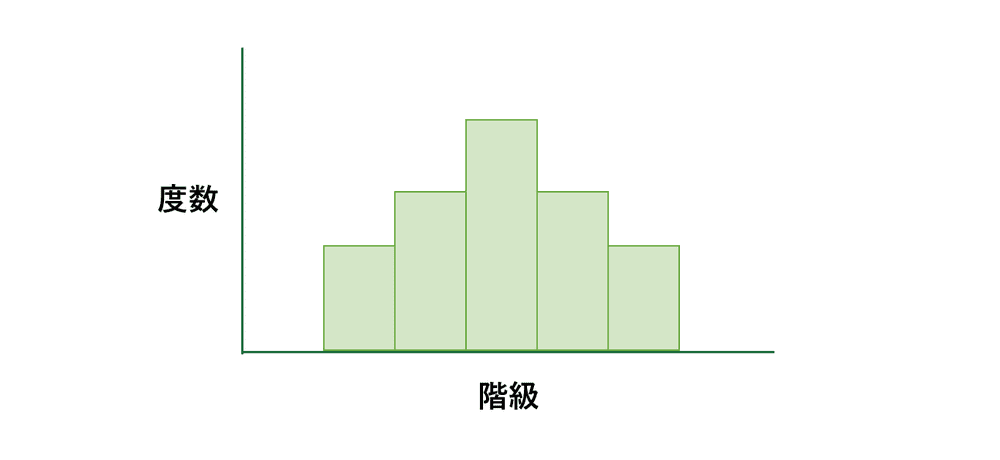
ヒストグラムは横軸に階級、縦軸に度数をとり、各階級の度数を長方形の柱で表します。
- 階級:度数を集計するためにグループ分けした区間
- 度数:各階級に属するデータの個数
階級の数を決める際、最大値や最小値、データ数などを参考にします。また「スタージェスの公式」を使うと目安となる階級の数が計算できます。
階級の幅が小さすぎたり、大きすぎたりしないようにしましょう。
ヒストグラムの例
実際にヒストグラムがどんなグラフか見てみましょう。
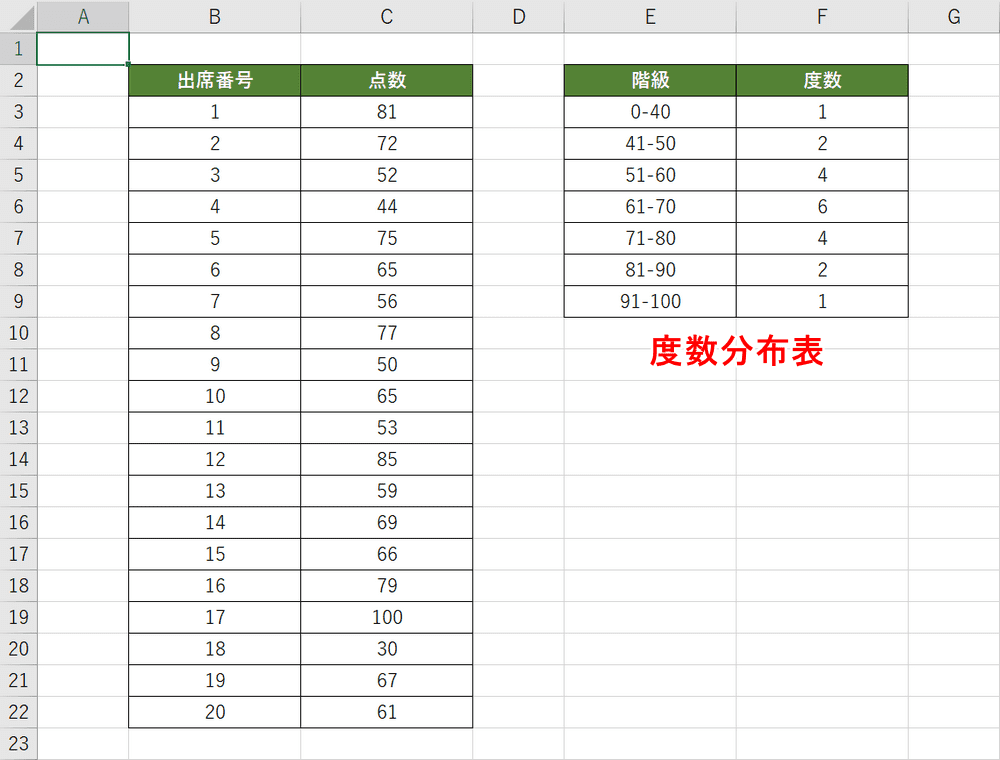
例えば20人のテストの点数を上図のB列のように入力したとします。点数を区間(階級)に分け、それぞれの階級に含まれる人数(度数)を整理したものが度数分布表です。
どの区間の人数が多い、少ないかは度数分布表で判断できますが、グラフにすることで分かりやすくしてみましょう。
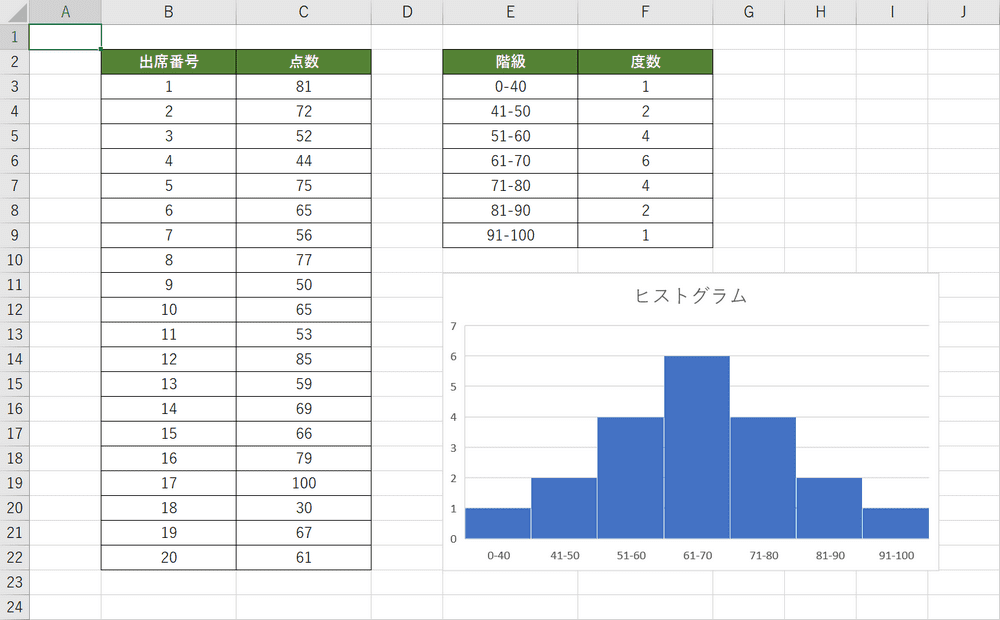
40点以下は1つの階級とし、それ以降は階級の幅を10としたヒストグラムを表してみました。
分布の中心付近の度数が多く、端にいくほど度数が少なくなっています。一般的に現われるヒストグラムです。
ヒストグラムの特徴(メリットやデメリット)
ヒストグラムを見れば分布のばらつき具合を確認できます。メリットとデメリットを知って使いこなしましょう。
ヒストグラムの利点(メリット)としては以下のようなものがあります。
- データの全体像、傾向を感覚的に把握しやすい
- 異常値を発見できる
ヒストグラムの注意点(デメリット)としては以下のようなものがあります。
- 個々のデータが見えにくくなる
ヒストグラムと棒グラフの違い
ヒストグラムと似ているグラフとして棒グラフがあります。棒グラフは、項目の値を棒で表したグラフです。両者の違いを確認して使い分けましょう。
| ヒストグラム | 棒グラフ | |
|---|---|---|
| 意味 | 度数分布表をグラフにしたもの | 項目の値を棒で表したグラフ |
| 使用目的 | 分布のばらつき具合を見る | 項目間を比較する |
| グラフの特徴 | 棒同士が隣接し、連続している | 棒同士が独立し、隙間が空いている |
| 横軸 | 階級 | 任意 |
| 縦軸 | 度数 | 任意 |
Excelによるヒストグラムの作成手順
Excel 2016から追加された機能を使ってヒストグラムを作成する手順を紹介します。Excel 2013以前では直接ヒストグラムを挿入できませんのでご注意ください。
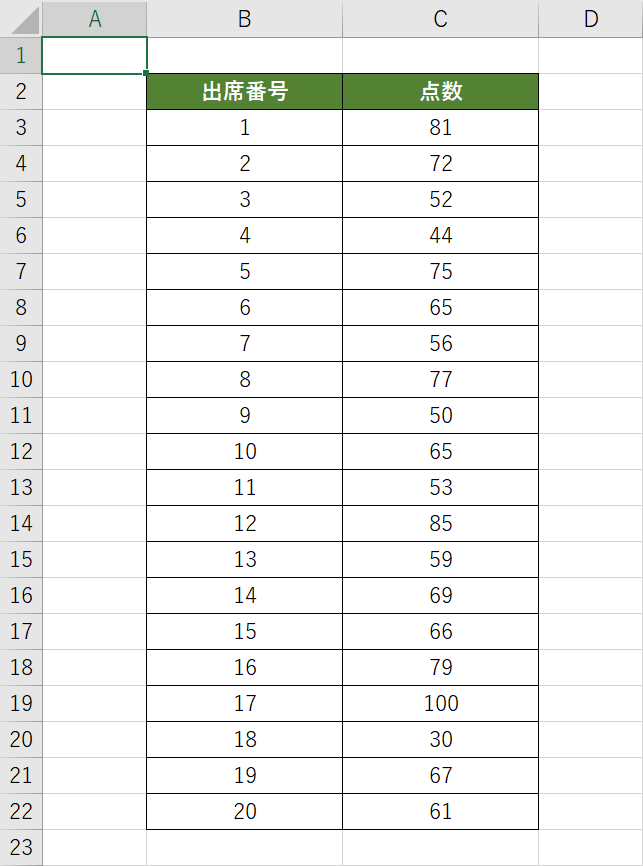
上図は、生徒20名分のテストの点数(100点満点)を表にまとめています。点数の分布を区間にグループ化して表示してみましょう。
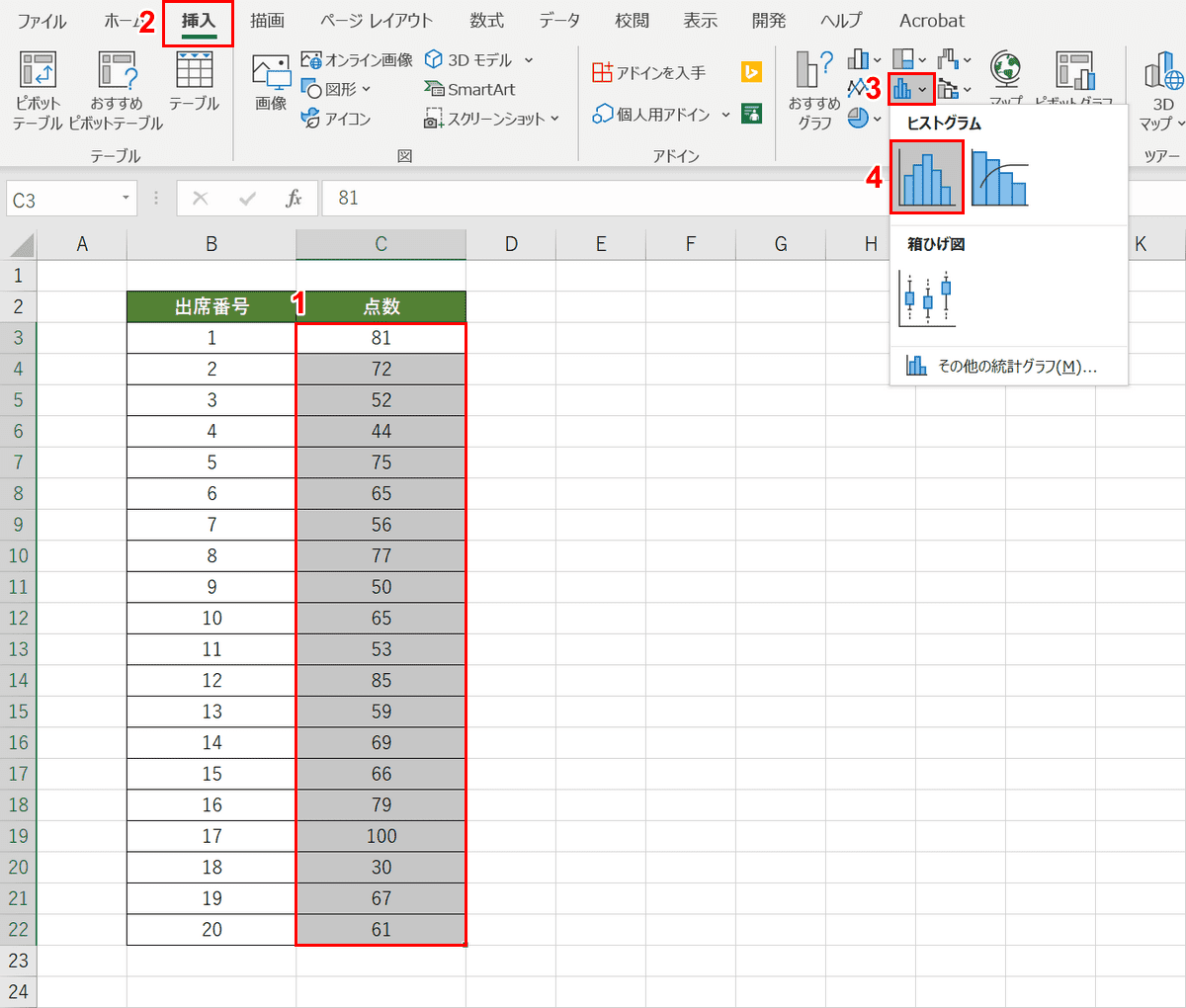
①【対象のデータ(例ではC3~C22セル)】を選択します。②【挿入】タブ、③【統計グラフの挿入】、④【ヒストグラム】の順に選択します。
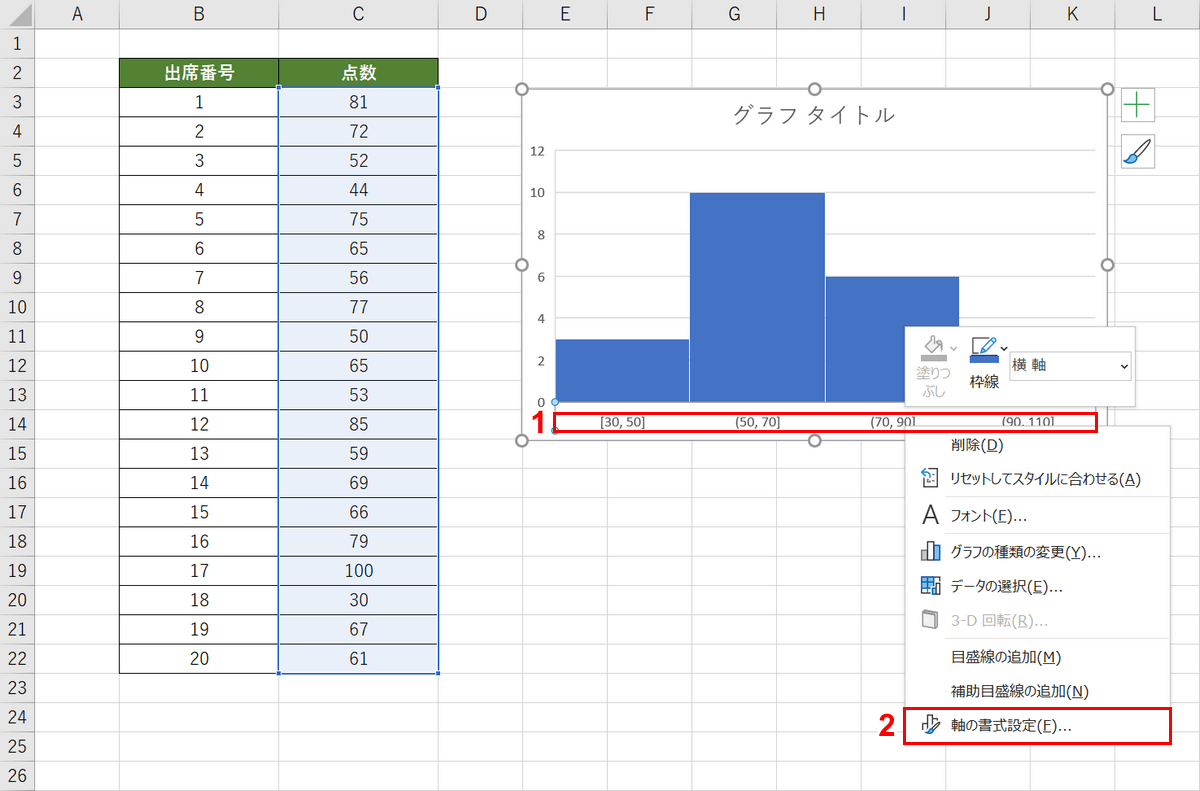
ヒストグラムがシートに挿入されました。階層の幅が自動で設定されたものなので30点以降は10点ごとになるように設定します。①グラフ内の【横軸】を選択し、【右クリック】します。②表示されたコンテキストメニューから【軸の書式設定】を選択します。
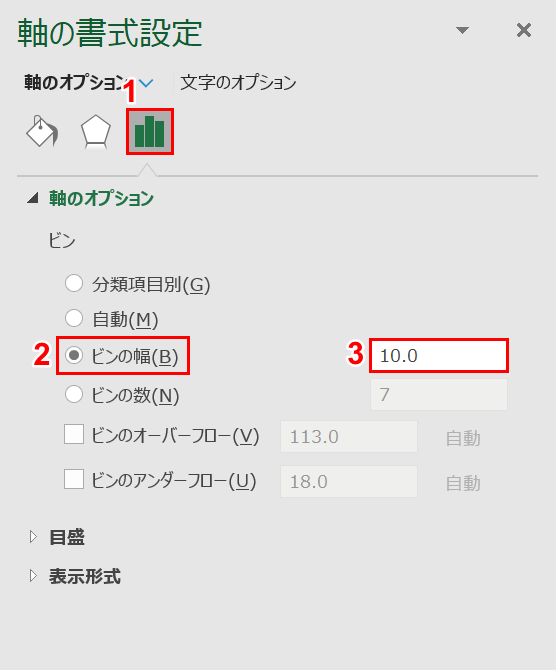
「軸の書式設定」が画面右側に表示されました。①【軸のオプション】、②「ビン」内の【ビンの幅】を選択し、③『10』と入力します。反映するために【Enter】キーを押します。
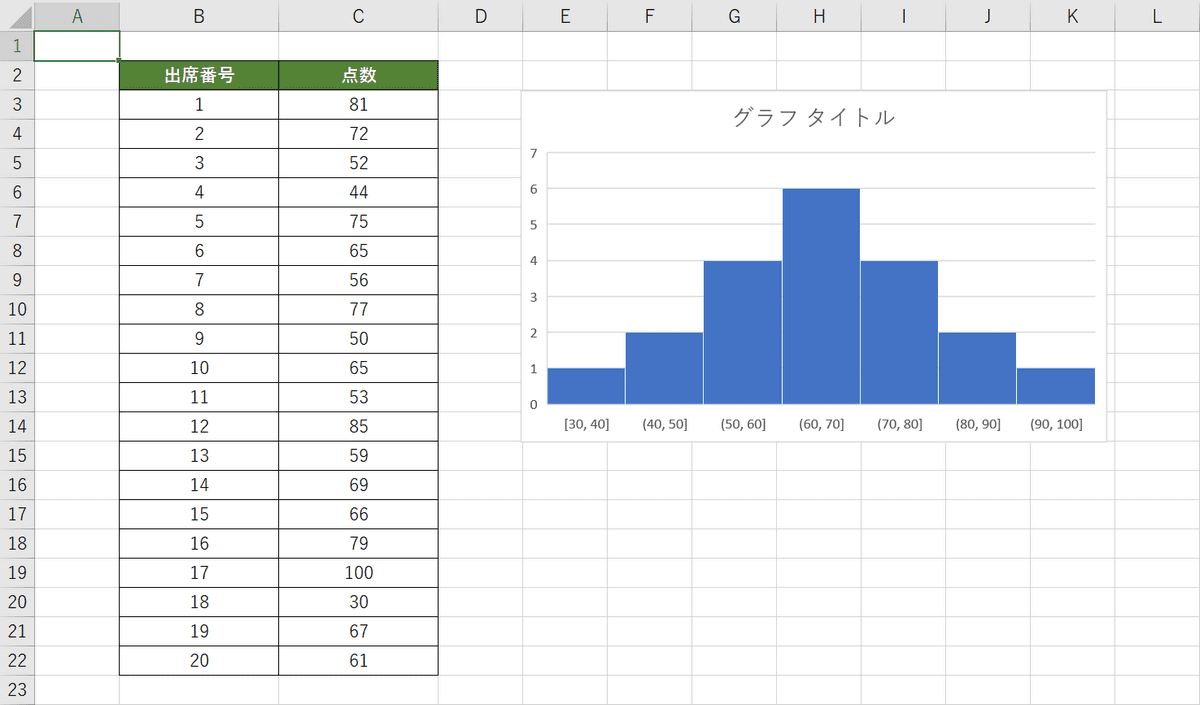
点数を10点ごとの区間にしたヒストグラムを作成することができました。
ヒストグラムの種類と見方
ヒストグラムは、分布の形状によって7種類に分類できます。形状を見ることでデータの特徴を把握できます。
一般型
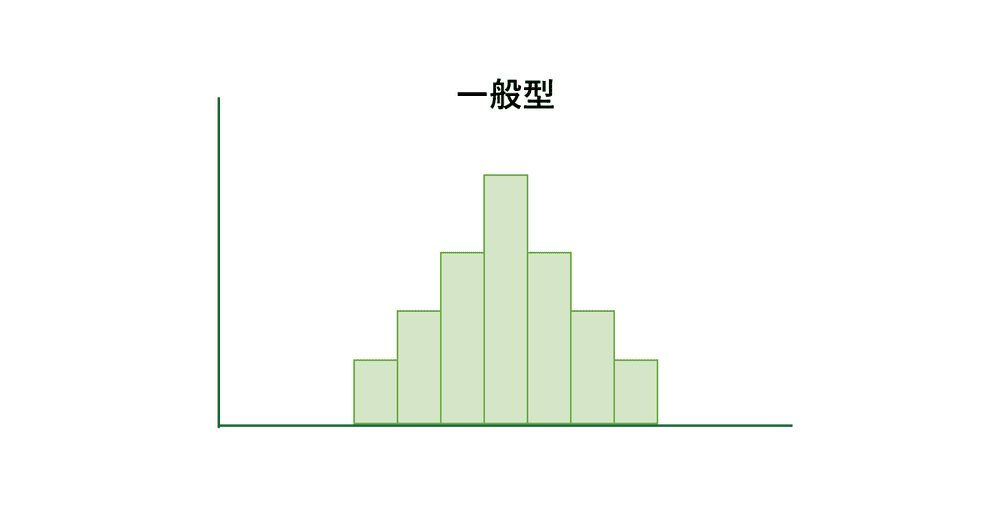
一般的に現われる形です。度数は、分布の中心付近が最も高く、中心から両端に離れるにしたがって徐々に少なくなり、左右対称になるのが特徴です。左右対称型、つり鐘型とも呼ばれます。
安定したデータで現れます。
くし歯型
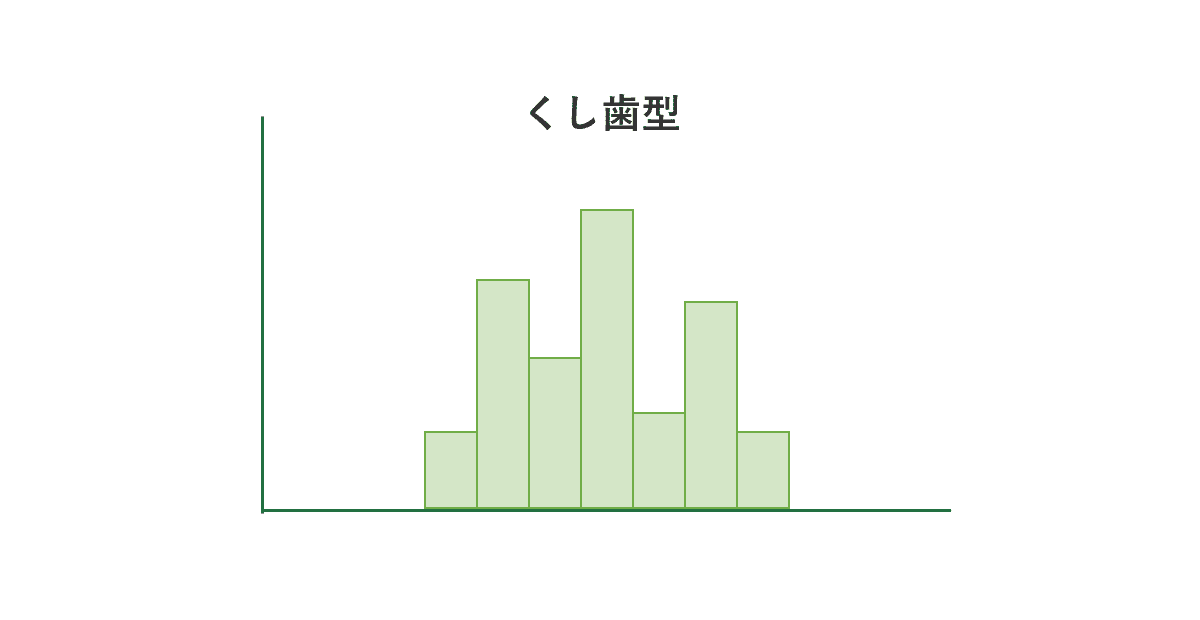
度数が階級ごとに多くなったり少なくなったりし、歯抜けやくしの歯の形になっているのが特徴です。歯抜け型とも呼ばれます。
階級の幅を整数にしていない、測定方法にクセがある場合などに現れます。
右すそ引き型(左すそ引き型)
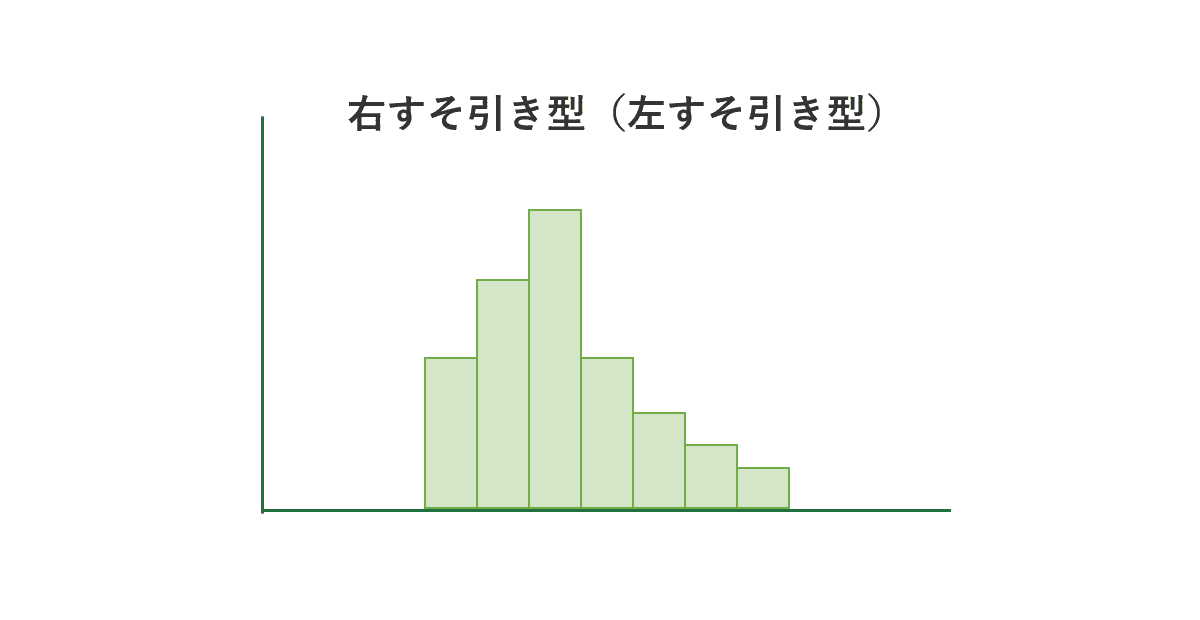
ヒストグラムの平均値が分布の中心よりも左右どちらかに寄っているのが特徴です。右すそ引き型の場合、度数は左側がやや急になり、右側はなだらかに少なくなっています。
上限もしくは下限が抑えられており、ある値以下、以上の値を取らない場合に現れます。
左絶壁型(右絶壁型)
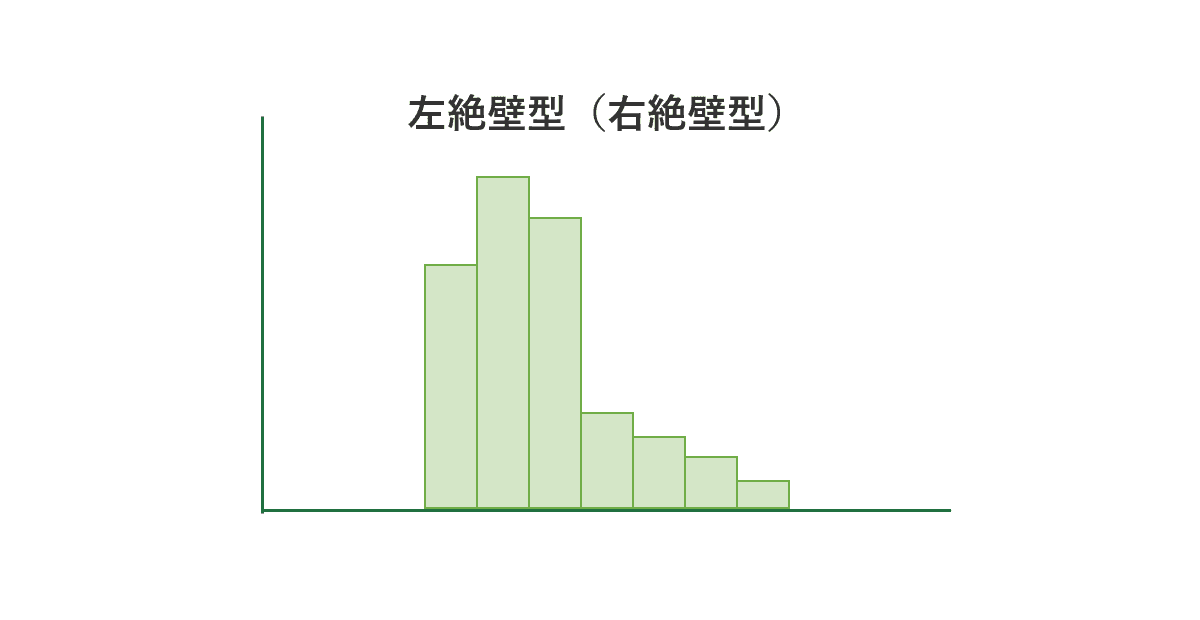
ヒストグラムの平均値が分布の中心よりも極端に左右どちらかに寄っているのが特徴です。左絶壁型の場合、度数は左側が急になり、右側はなだらかに少なくなっています。
データが選別されている時に現れやすいです。測定の間違いがないか確認してみましょう。
高原型
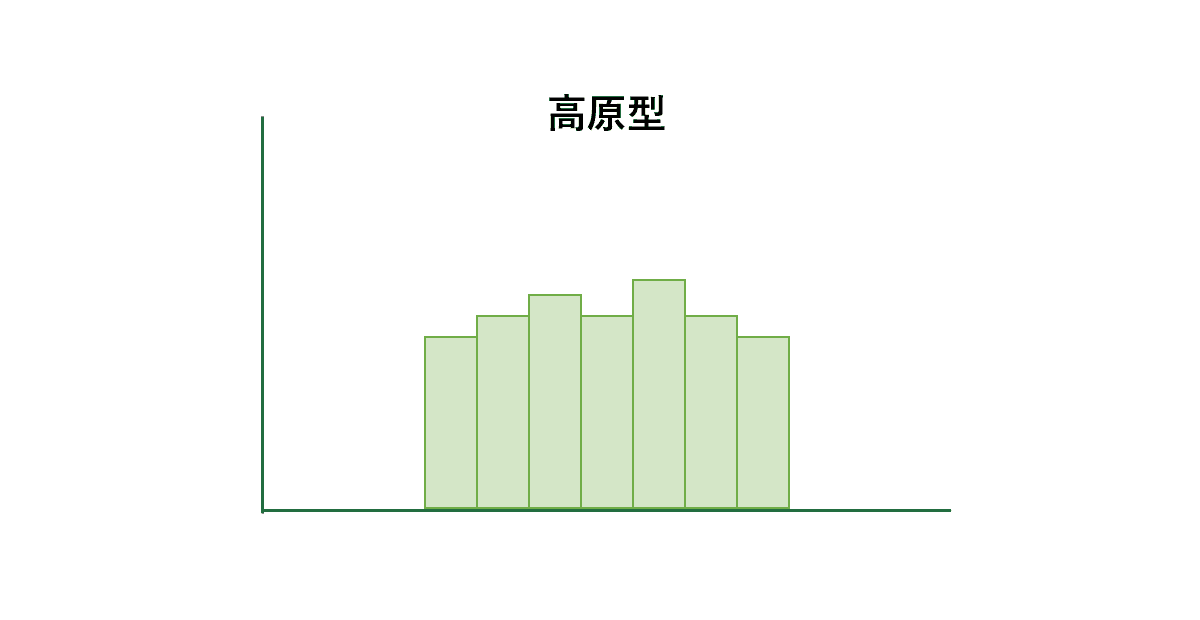
各階級に含まれる度数があまり変わらず、高原状になっているのが特徴です。
平均値が異なるいくつかの分布が混じっている場合に現れます。ヒストグラムをグループ分けして比較してみましょう。
ふた山型
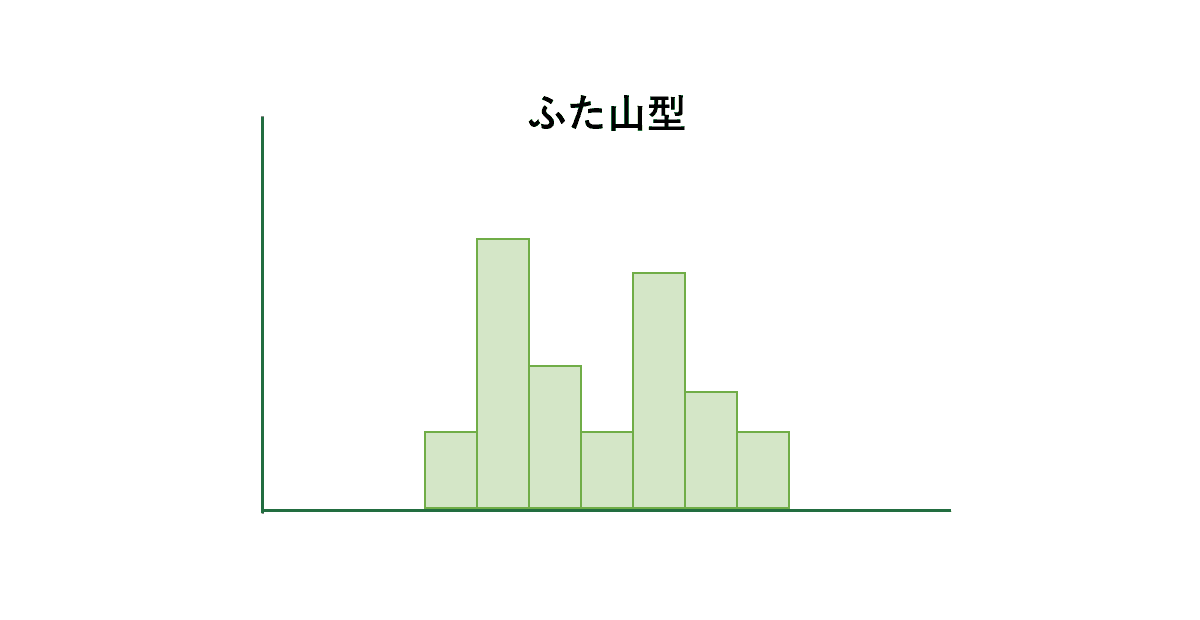
分布の中心付近の度数が少なく、左右に山があるのが特徴です。
平均値が異なる2つの分布が混じっている場合に現れます。元のデータを確認してみましょう。
離れ小島型
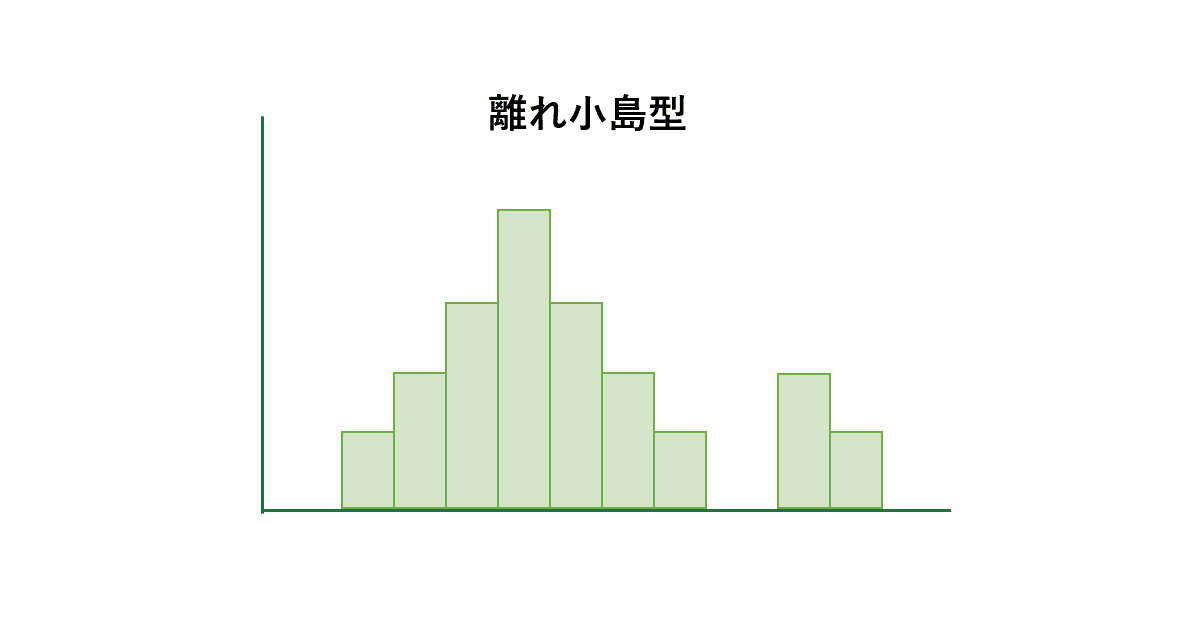
ヒストグラムの右の端、もしくは左の端に離れ小島があるのが特徴です。
異なった分布からのデータが少し混じっている場合に現れます。測定に誤りがないか調べてみましょう。
ヒストグラムからわかること
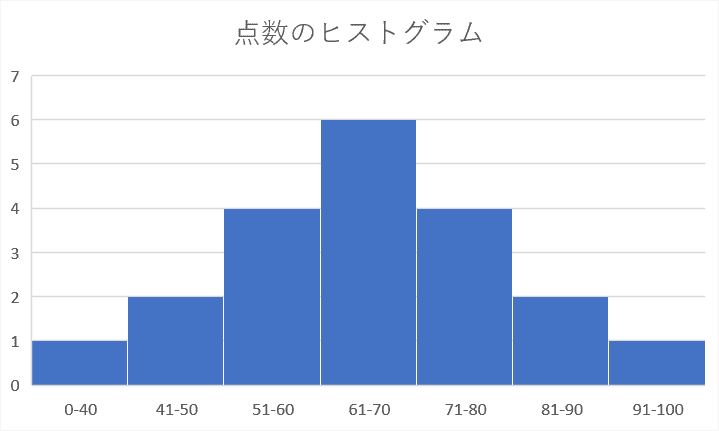
元のデータがなくヒストグラムしかない場合、平均値や中央値などを求めるにはどうしたらいいでしょうか?計算の仕方を説明します。
平均値を求める
ヒストグラムから平均値を求める方法を紹介します。
平均値を求めるには、「(階級値×度数)の合計 ÷ 度数の合計」という公式を使用します。
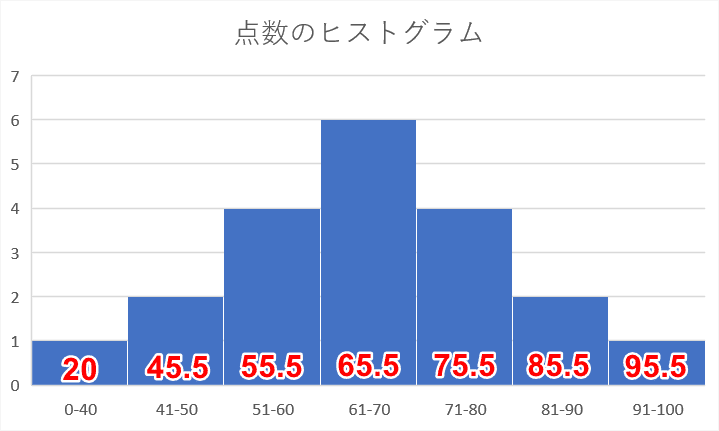
まず階級値を求めます。階級値は「(階級の最大値+階級の最小値)÷ 2」で求めることができます。上図のヒストグラムに赤字で階級値を入力しました。
度数の合計は「20」です。公式に入れて計算してみましょう。
「((20×1)+(45.5×2)+(55.5×4)+(65.5×6)+(75.5×4)+(85.5×2)+(95.5×1)) ÷ 20」の計算結果は「64.725」になりました。実際にデータから平均値を求めた場合と誤差が発生します。
中央値を求める
中央値(メジアン)はデータを値の大きさの順に並べたとき、中央の位置にくる値です。
上記のヒストグラムには20のデータがあります。点数の低い方から10番目と11番目の階級値の平均をとります。「(65.5 + 65.5)÷ 2」の計算結果は「65.5」になりました。
最頻値を求める
最頻値(モード)は最も度数が多い階級の階級値をいいます。
ヒストグラムから最も度数が多い階級は「61-70」です。その階級値「65.5」が最頻値になりました。
標準偏差を求める
ヒストグラムから標準偏差を求める場合、階級値を使用します。階級値を使用するため実際のデータから計算した場合と比べて誤差が発生します。
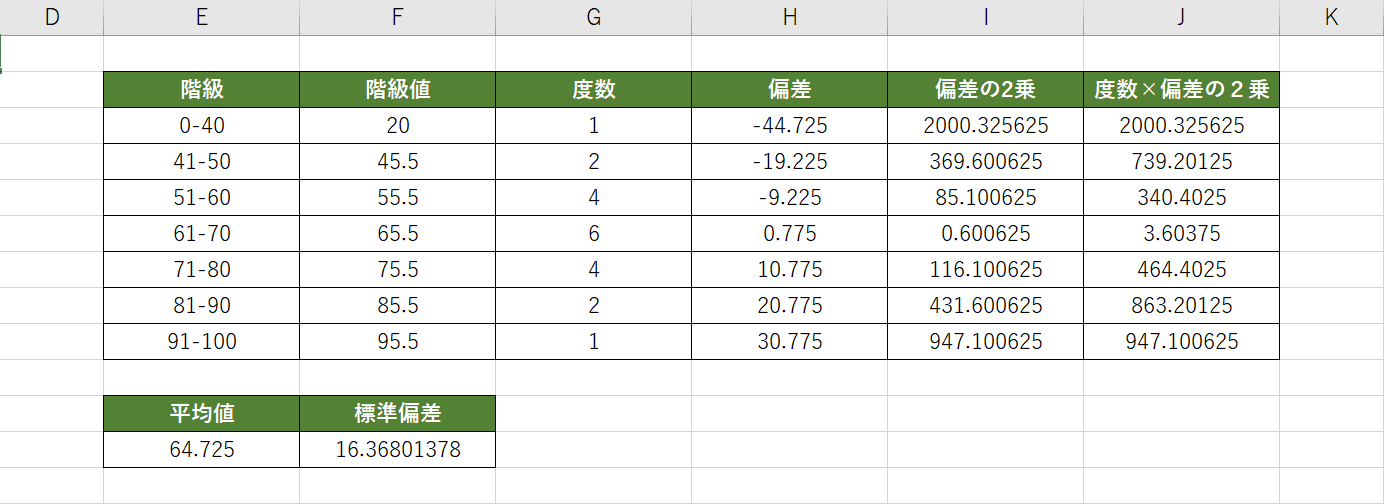
計算しやすいように表にまとめます。「階級」「度数」「階級値」「平均値」は上記で求めることができました。
偏差は各階級値と平均値の差です。その偏差を2乗し、度数とかけ合わせます。「度数×偏差の2乗」の合計をデータ数(20)で割った値を正の平方根で計算します。
「16.36801378」が例のヒストグラムから求めた標準偏差です。
Excelで標準偏差を計算する詳しい方法は下記の記事で紹介していますのでご参考ください。
標準偏差をエクセルの関数で求める方法とグラフの作り方(散布図)
ヒストグラムと正規分布曲線を重ねる方法
Excelを使ってヒストグラムと一緒に正規分布曲線を重ねてグラフにする方法を説明します。
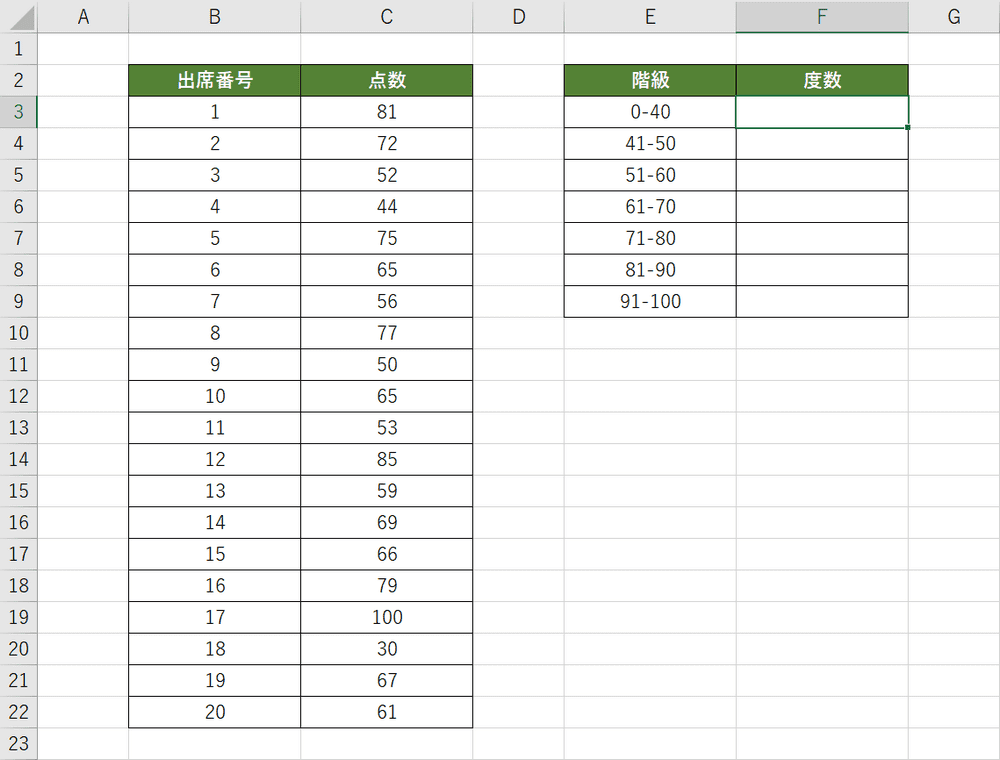
まず度数分布表を作成します。今回は40点以下で1つの階級にし、40点以降は階級の幅を10にしています。まず階級に含まれる度数を求めます。
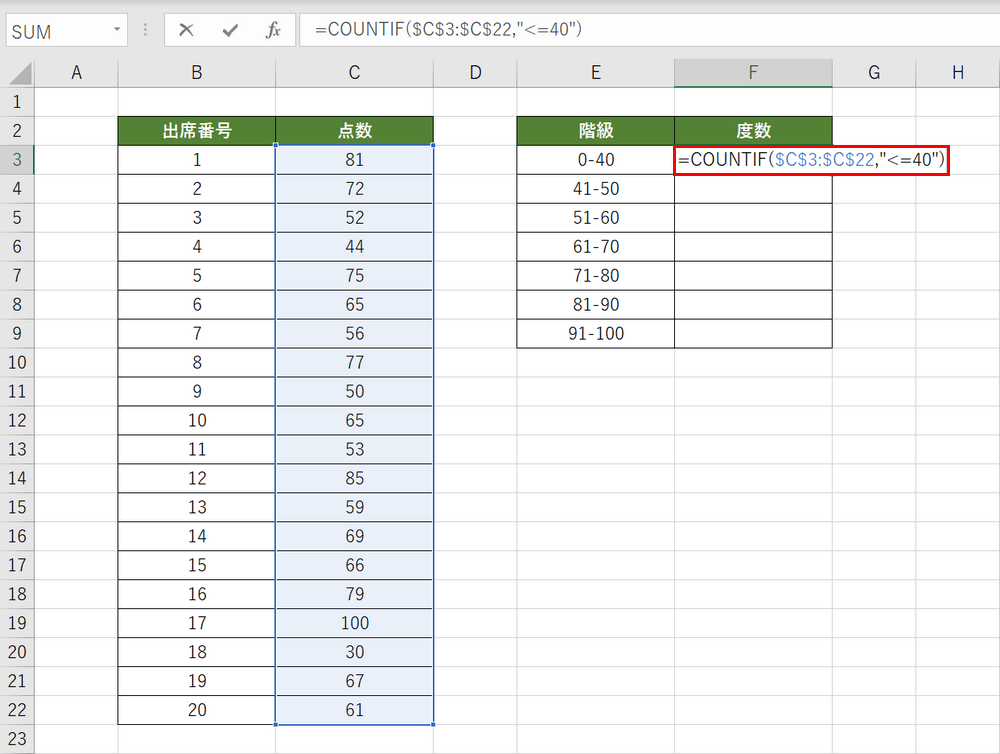
40点以下のテストのデータをCOUNTIF関数を使ってカウントします。F3セルを選択し、『=COUNTIF($C$3:$C$22,"<=40")』と入力し、Enterを押します。
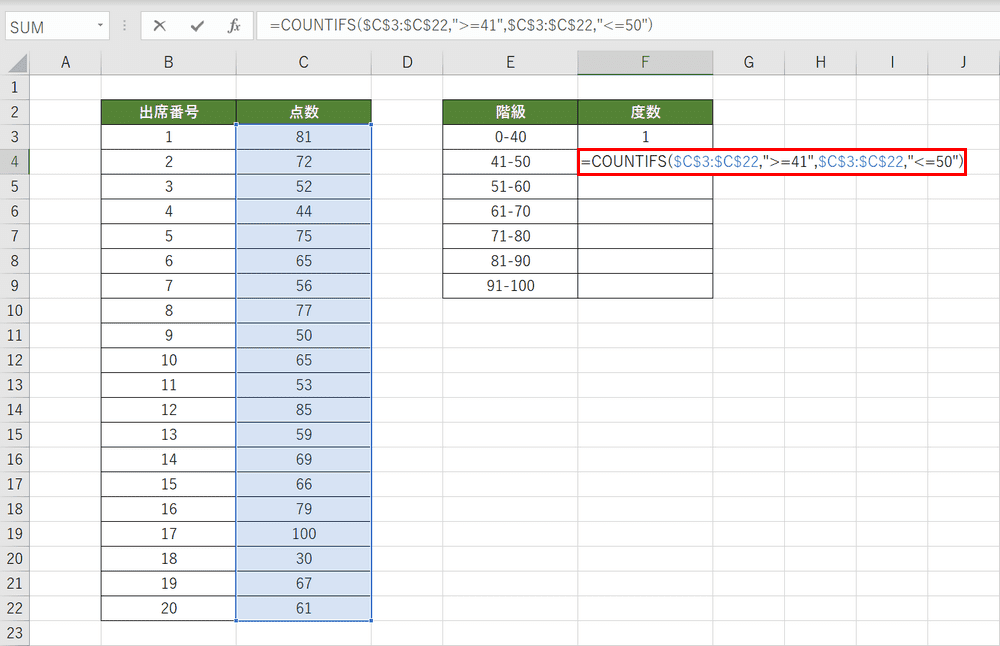
41点以上、50点以下のテストのデータをCOUNTIFS関数を使ってカウントします。F4セルを選択し、『=COUNTIFS($C$3:$C$22,">=41",$C$3:$C$22,"<=50")』と入力し、Enterを押します。
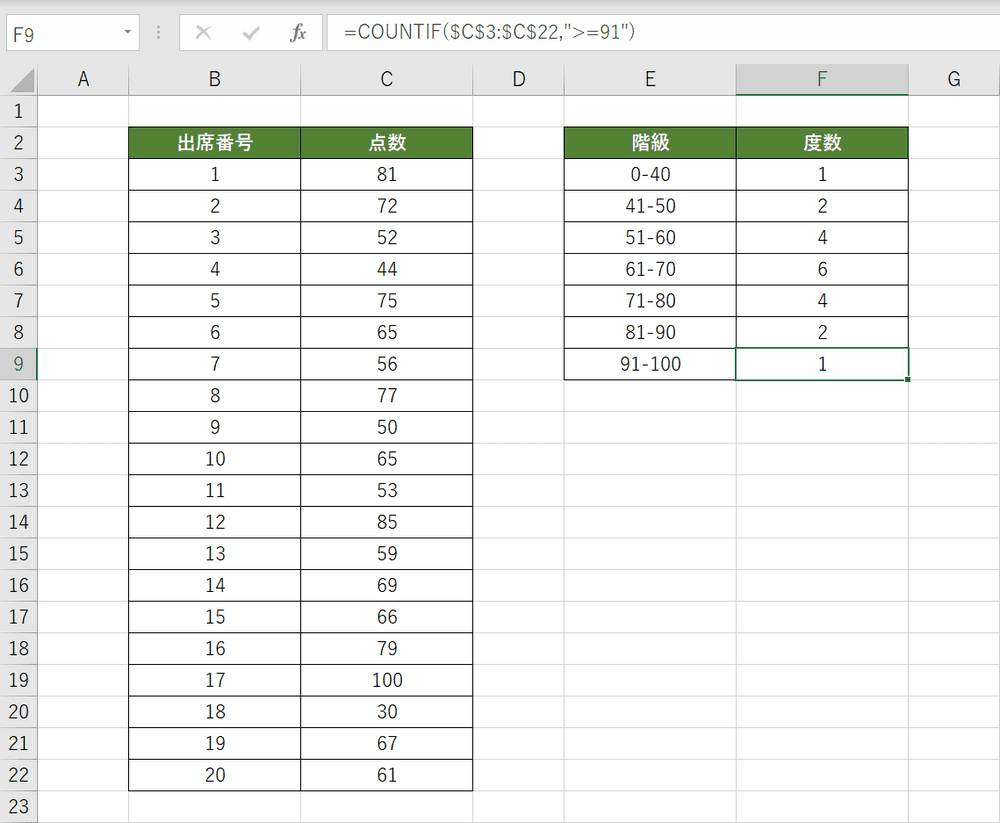
上記と同じようにCOUNTIFS関数で度数をカウントしていきます。度数分布表が完成しました。
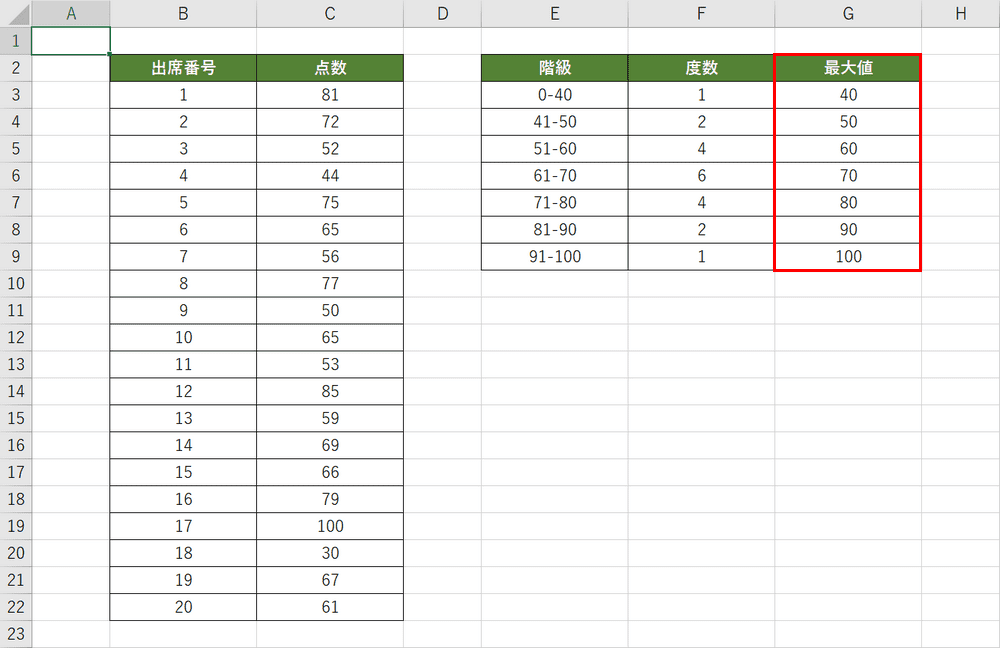
階級ごとの最大値をG列に用意します。
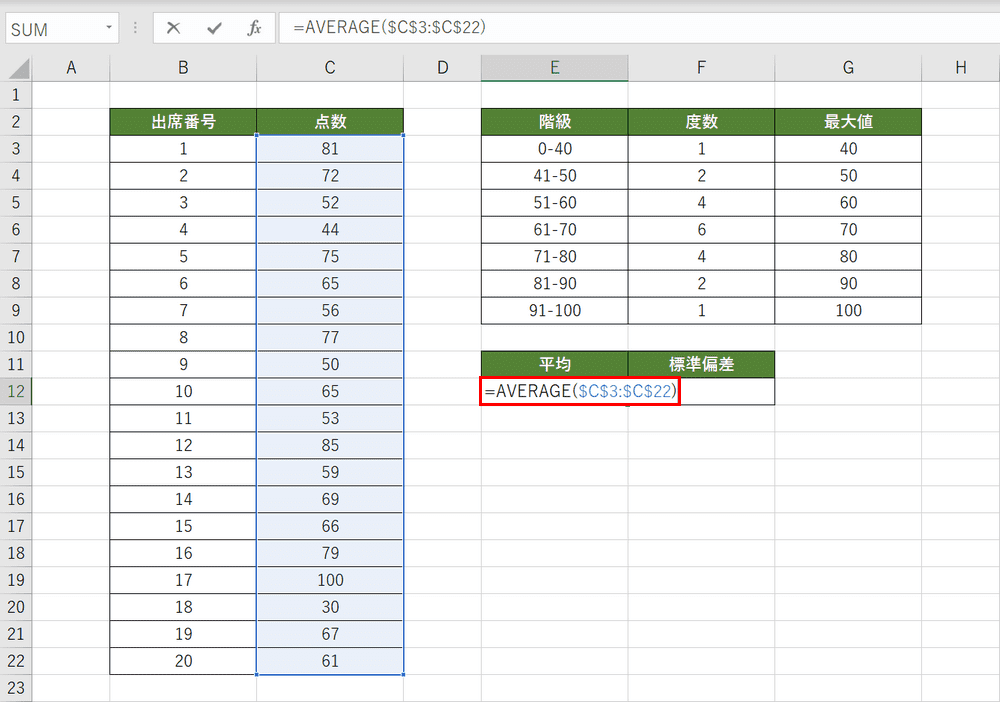
データの平均を求めます。E12セルを選択し、『=AVERAGE($C$3:$C$22)』と入力し、Enterを押します。
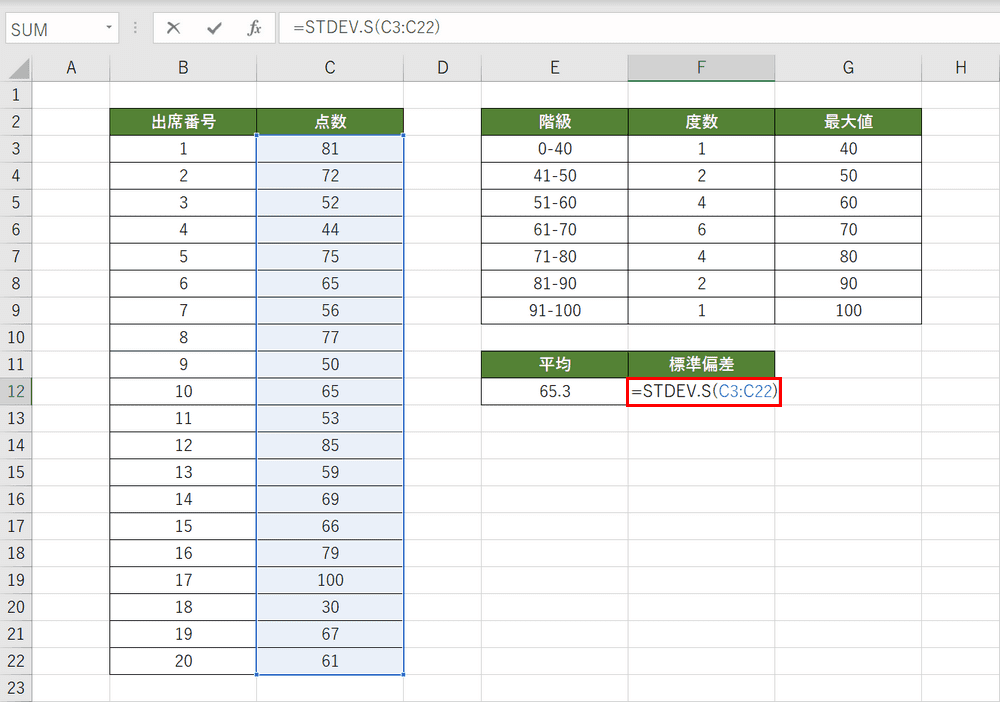
データの標準偏差を求めます。F12セルを選択し、『=STDEV.S(C3:C22)』と入力し、Enterを押します。
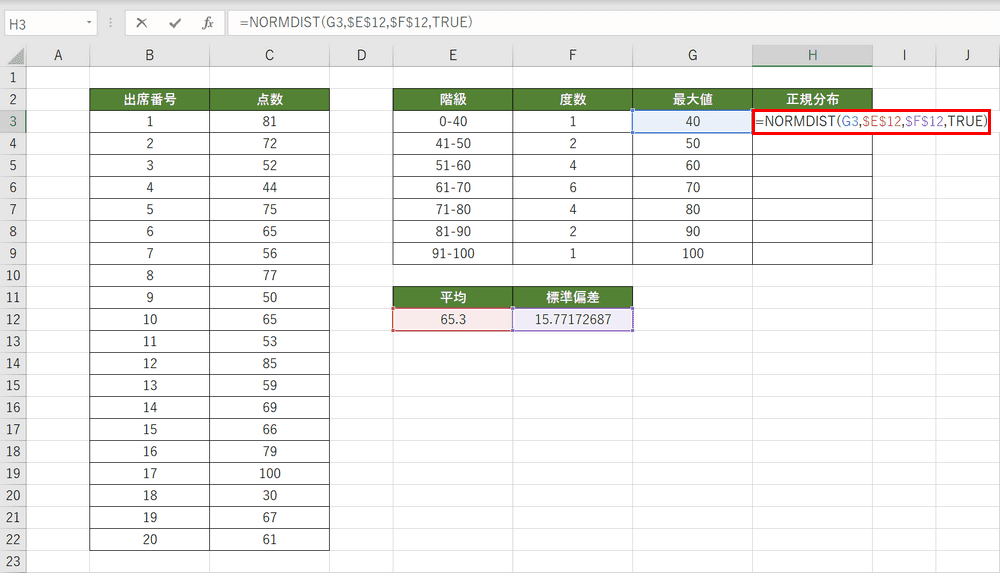
この例では階級における最大値から正規分布を求めています。他にも正規分布を求める方法はありますので目的に合わせてみてください。
階級における最大値の正規分布をNORMDIST関数で求めます。H3セルを選択し、『=NORMDIST(G3,$E$12,$F$12,TRUE)』と入力します。数式を確定するためにEnterを押します。
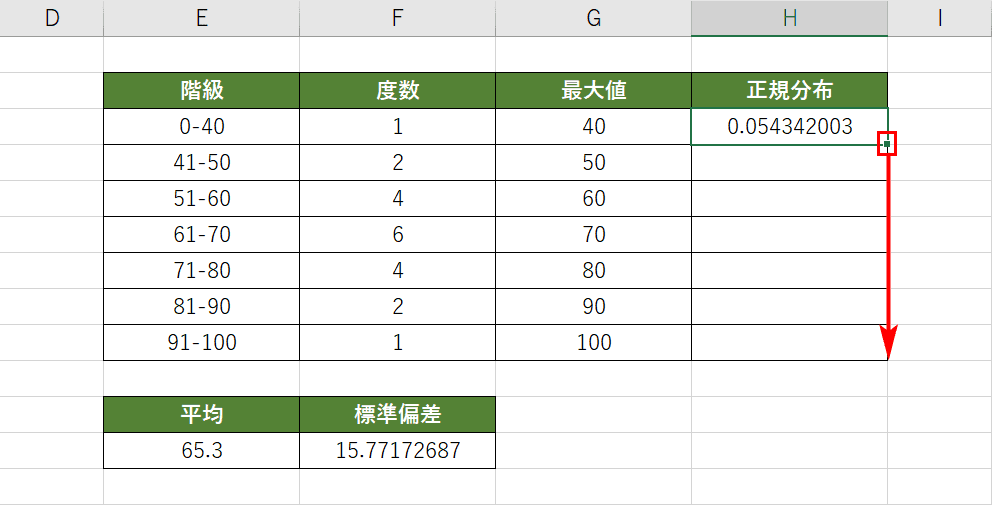
H3セル右下を表の下までドラッグしてオートフィルで数式をコピーします。
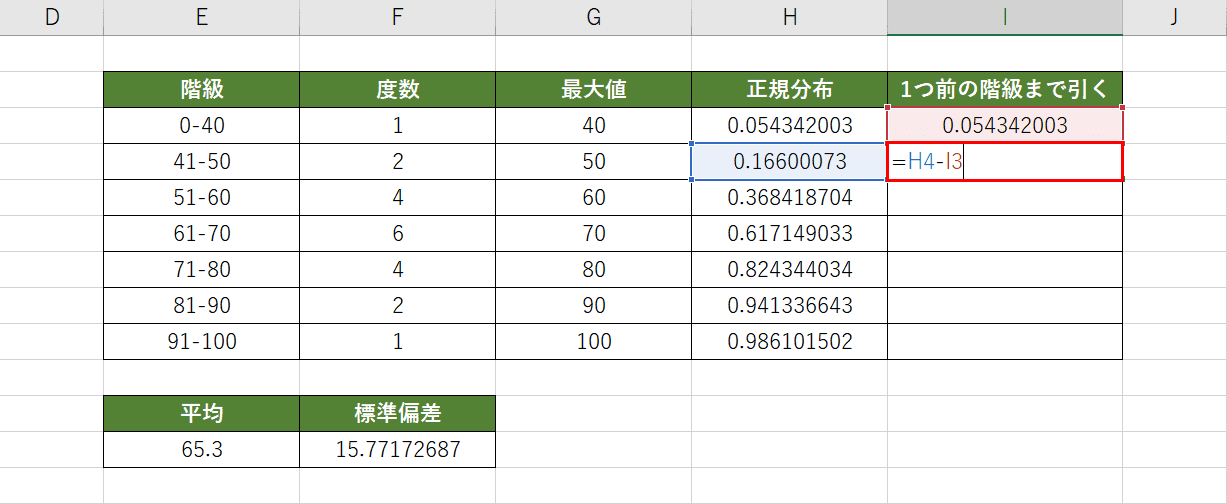
さらにI列にH列で求めた正規分布を1つ前の階級までを引いたものを計算していきます。「0-40」の階級はそのまま使用します。I4セルを選択し、『=H4-I3』と入力してEnterを押します。
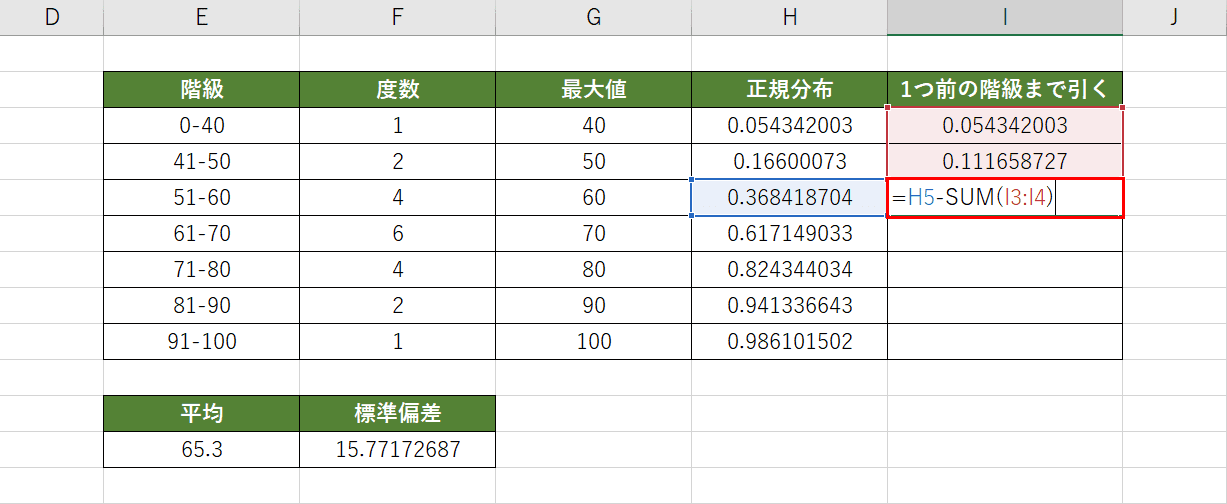
次に階級「51-60」はそれまでの階級の正規分布の合計を引き算します。I5セルを選択し、『=H5-SUM(I3:I4)』と入力してEnterを押します。
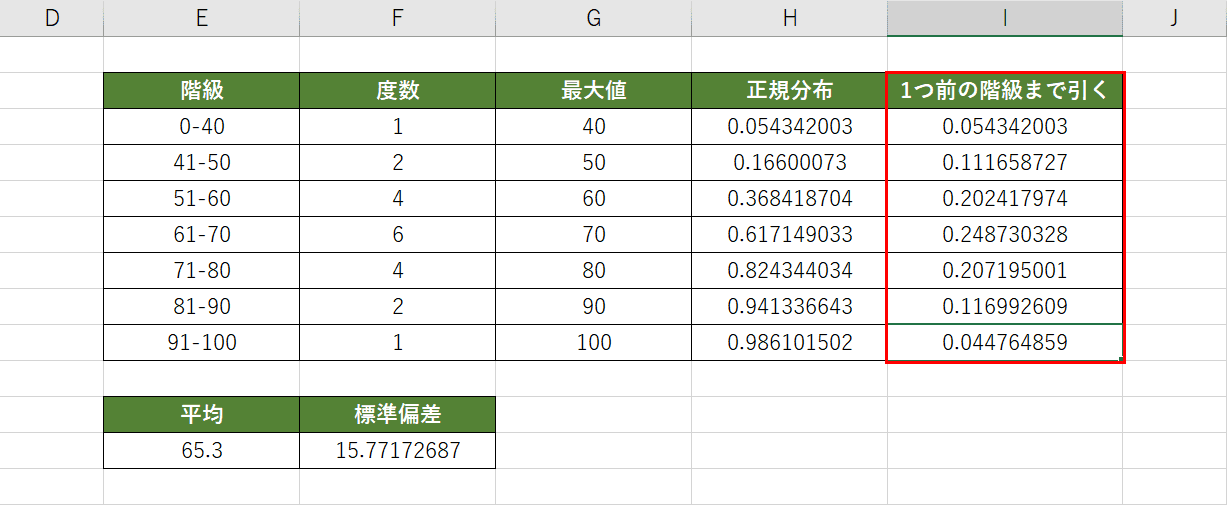
上記と同じように1つ前までの階層の正規分布を引いていきます。
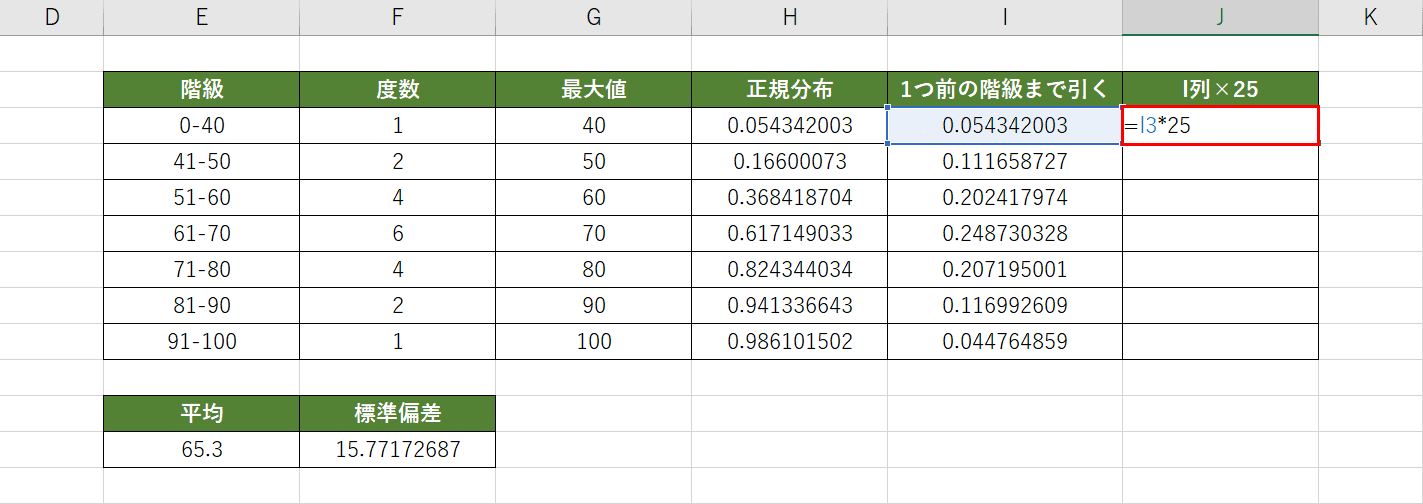
J列を用意し、I列で求めた結果を25倍にします。I列の結果をグラフにすると度数に比べて小さすぎるので25倍して調整しています。
J3セルを選択し、『=I3*25』と入力してEnterを押します。
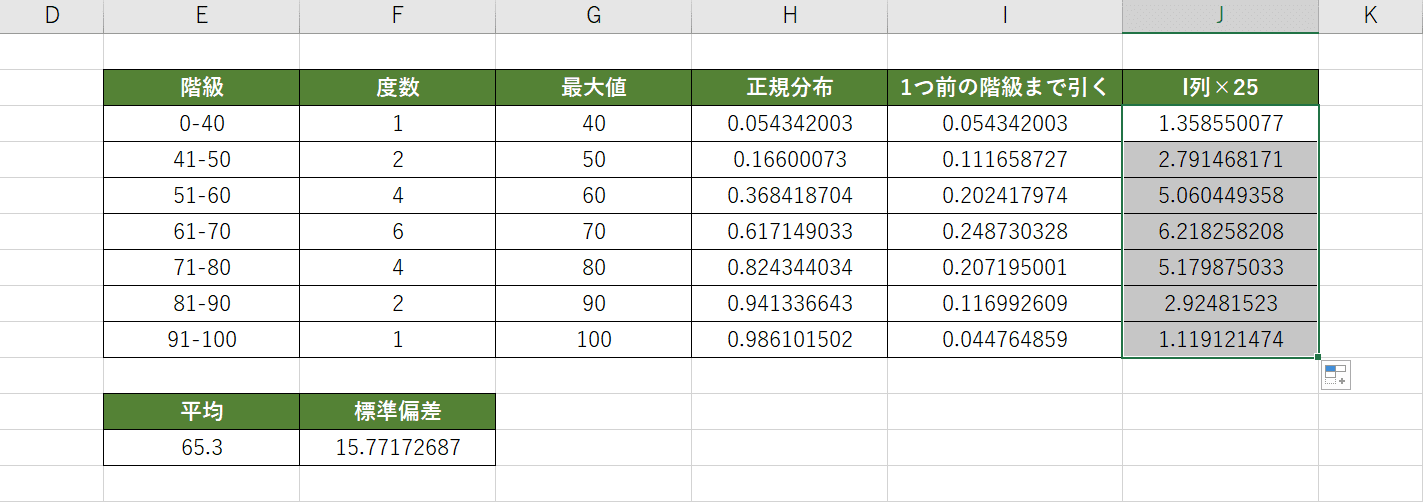
オートフィルでJ3セルの数式をコピーしてJ列を求めます。
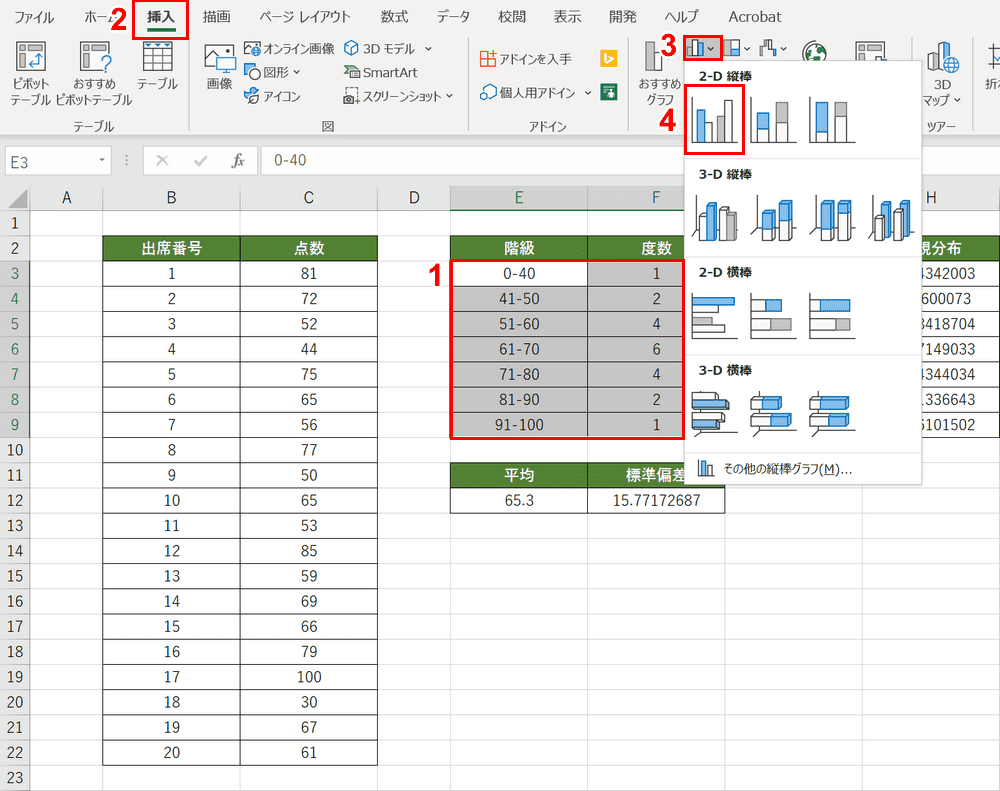
①階級と度数を選択し、②【挿入】タブ、③【縦棒/横棒グラフの挿入】、④【集合縦棒】の順に選択します。
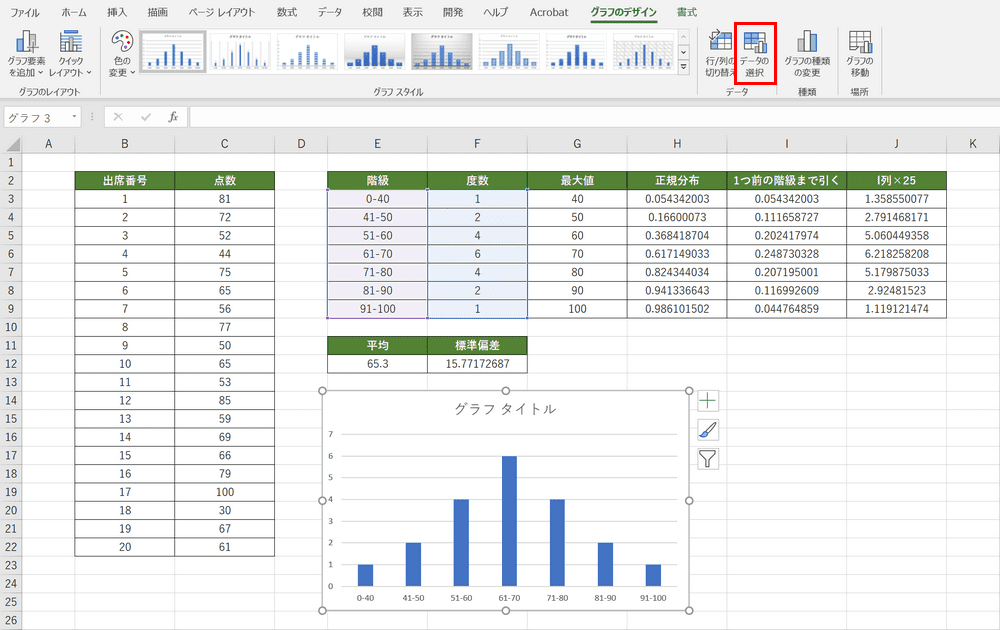
集合縦棒のグラフがシートに挿入されました。【データの選択】を選択します。
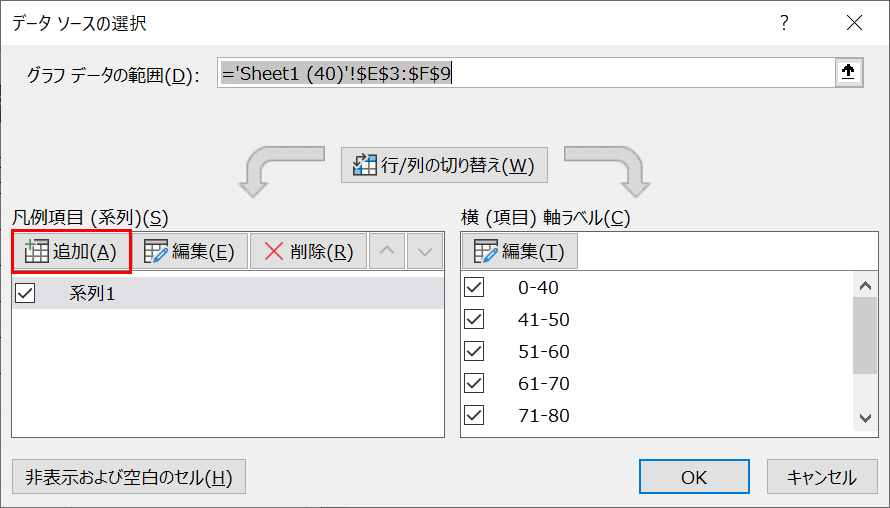
「データソースの選択」ダイアログボックスが表示されます。「凡例項目(系列)」の【追加】ボタンを押します。
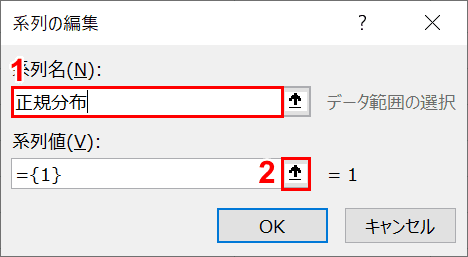
「系列の編集」ダイアログボックスが表示されます。①「系列名」に『正規分布』と入力し、②「系列値」右端の【↑】ボタンを押します。
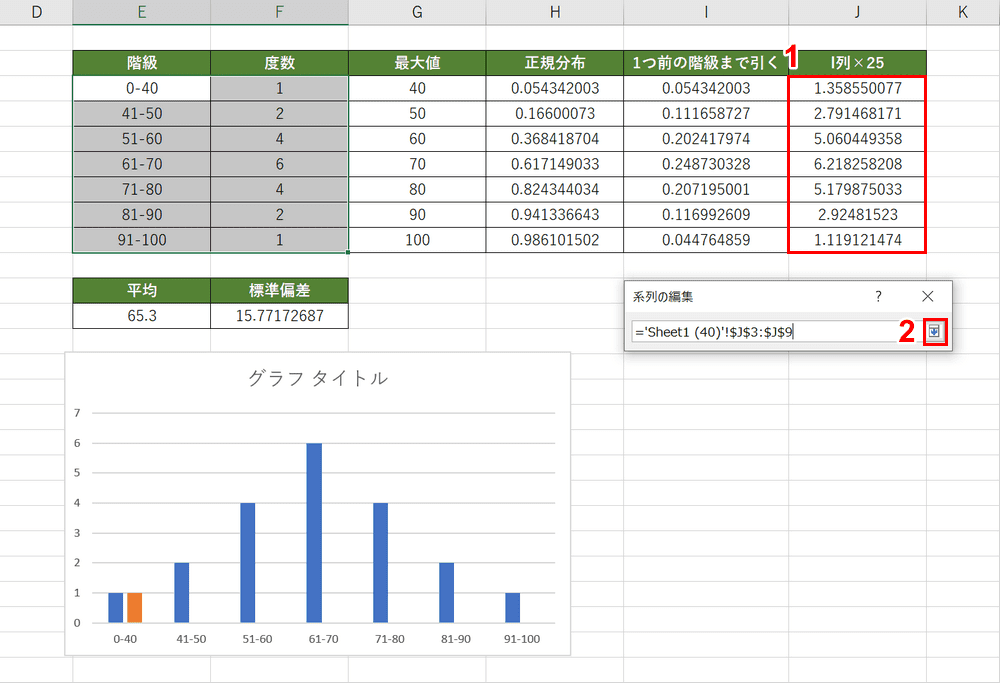
①J列で求めた結果を選択し、②「系列の編集」ダイアログボックス内の【↓】ボタンを押します。
「系列の編集」ダイアログボックス内の【OK】ボタンを押します。
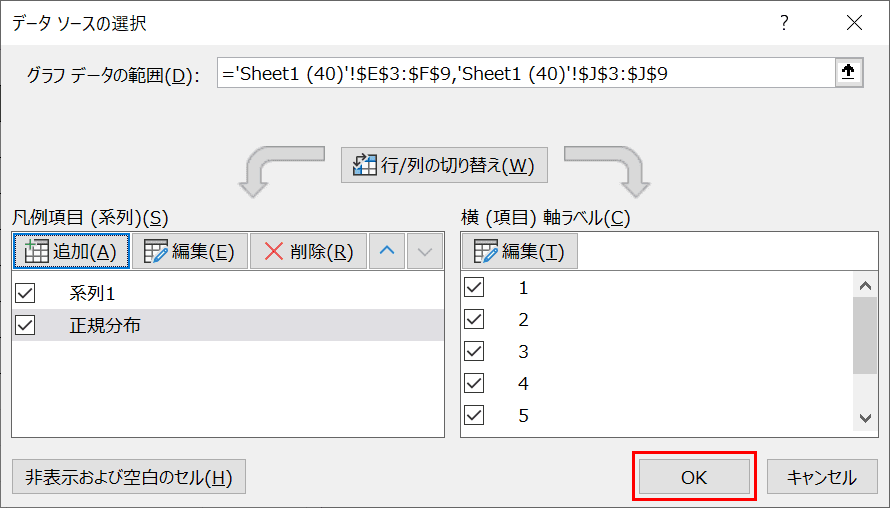
「データソースの選択」ダイアログボックスに戻るので【OK】ボタンを押します。
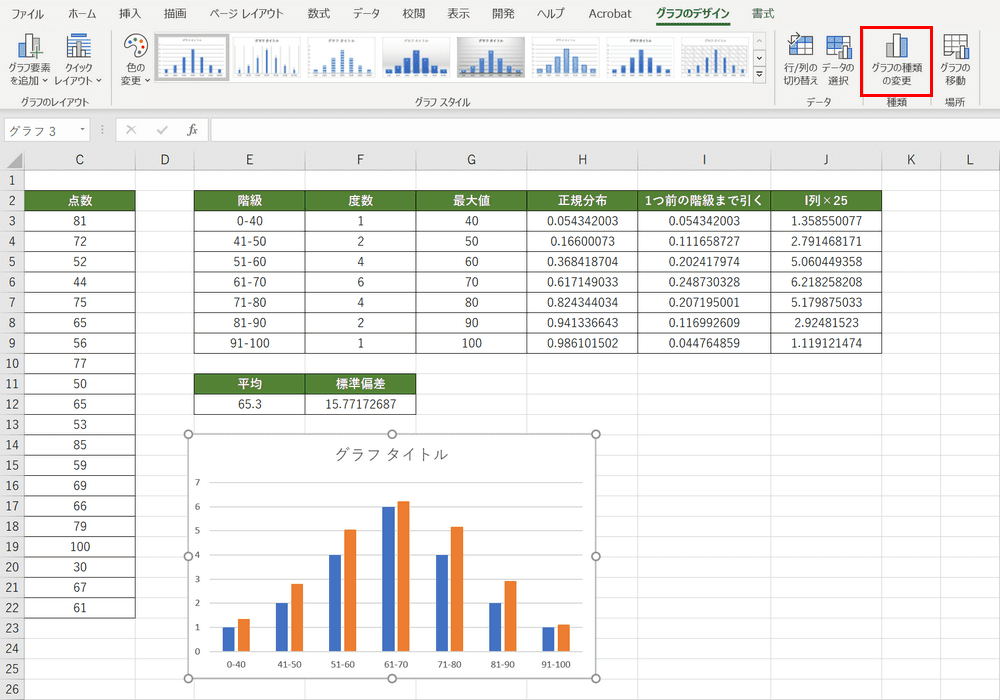
【グラフの種類の変更】を選択します。
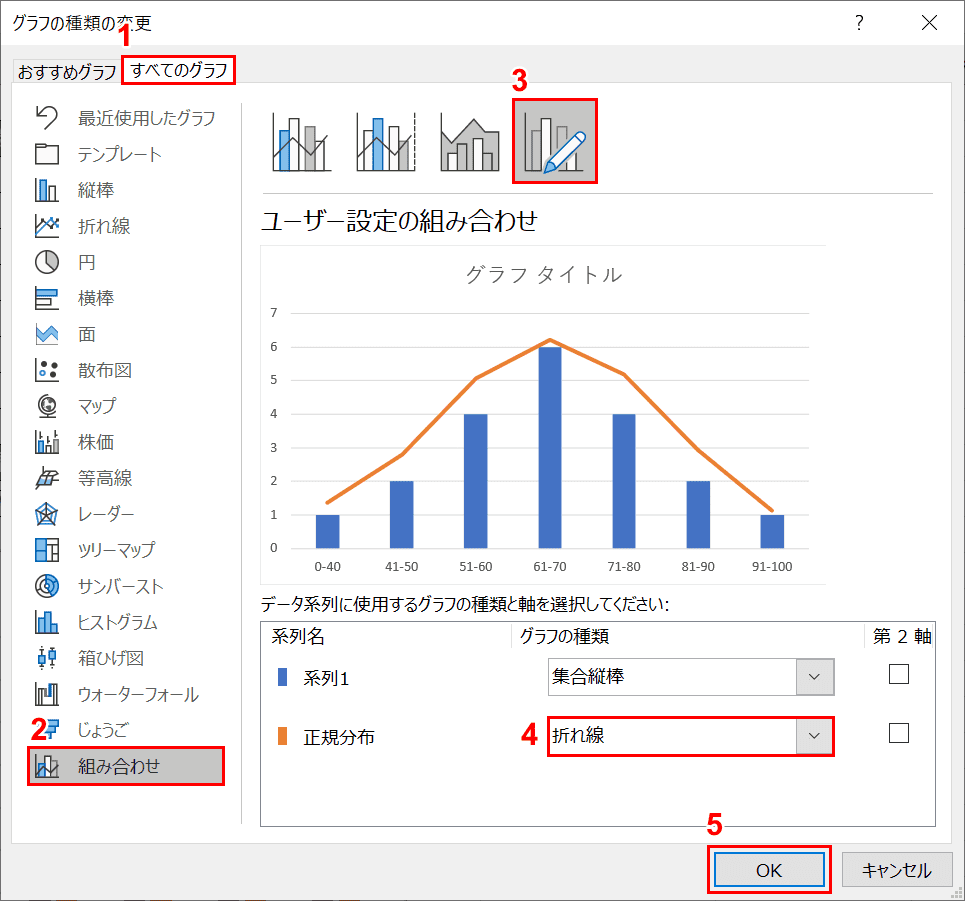
「グラフの種類の変更」ダイアログボックスが表示されます。①【すべてのグラフ】、②【組み合わせ】、③【ユーザー設定の組み合わせ】の順に選択します。④系列名「正規分布」のグラフの種類を【折れ線】に変更して⑤【OK】ボタンを押します。
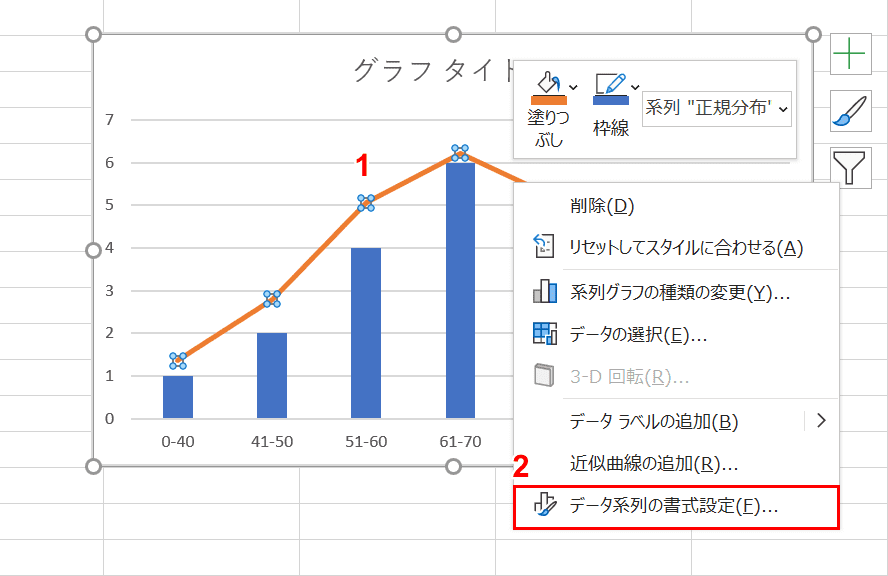
①グラフ内の折れ線グラフを選択し、【右クリック】します。②表示されたコンテキストメニューから【データ系列の書式設定】を選択します。
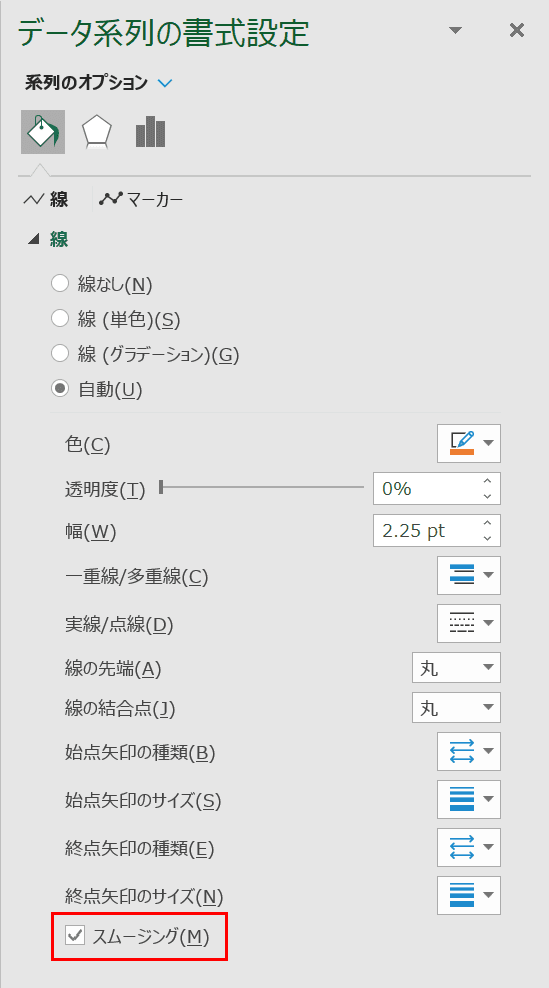
画面右側に「データ系列の書式設定」が表示されました。【スムージング】にチェックを入れます。
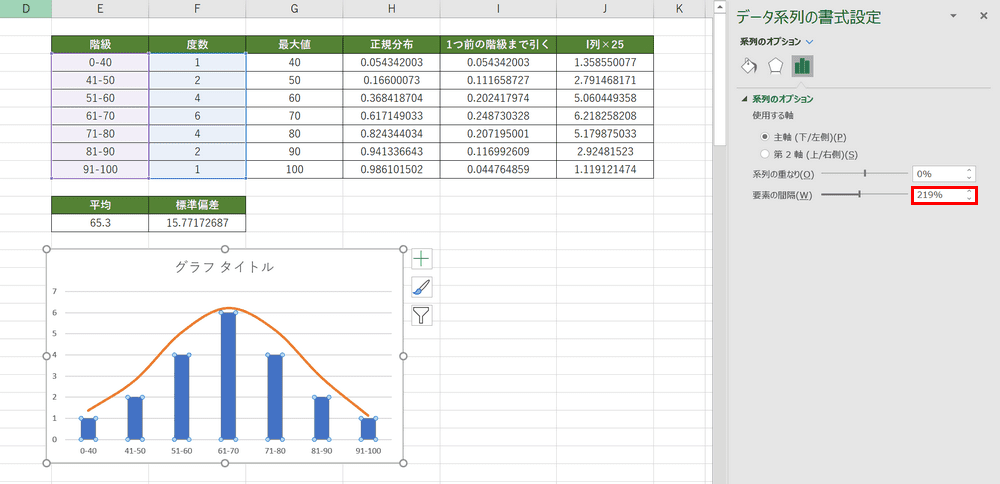
折れ線がスムーズになりました。グラフ内の縦棒を選択し、「データ系列の書式設定」内の「要素の間隔」に『1』と入力してEnterを押します。
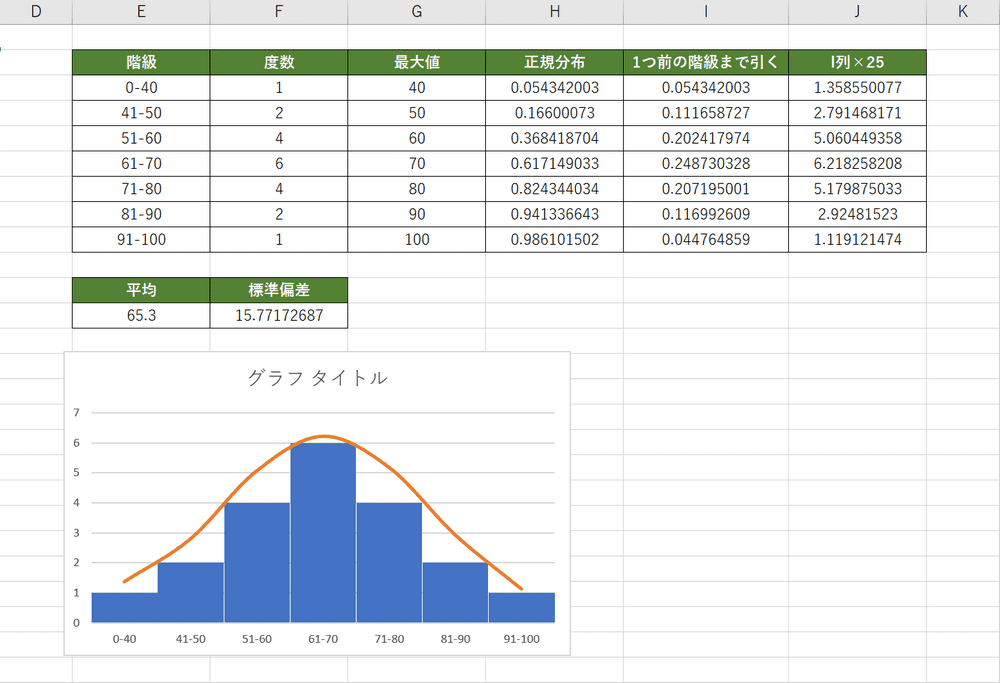
ヒストグラムと正規分布曲線を1つのグラフで表すことができました。
Excelで正規分布曲線を作成する詳しい方法は下記の記事で紹介していますのでご参考ください。
