- 公開日:
エクセルの近似曲線に関する情報まとめ
この記事では、エクセルの近似曲線に関する様々な情報をまとめて紹介します。
近似曲線とは、エクセルのグラフにおいてデータの推移をおおまかに表した線を指し、「線形」や「指数」など様々な近似曲線をグラフに追加することが出来ます。
今回は主に「線形」の近似曲線を使ってご説明しています。
近似曲線が利用できるグラフの種類
近似曲線は一部のグラフでは利用できません。
近似曲線を追加できるグラフは、以下の通りです。
- 縦棒グラフ
- 横棒グラフ
- 折れ線グラフ
- 散布図
- バブルチャート
散布図に近似曲線を追加する方法
散布図に近似曲線を追加する方法をご説明します。
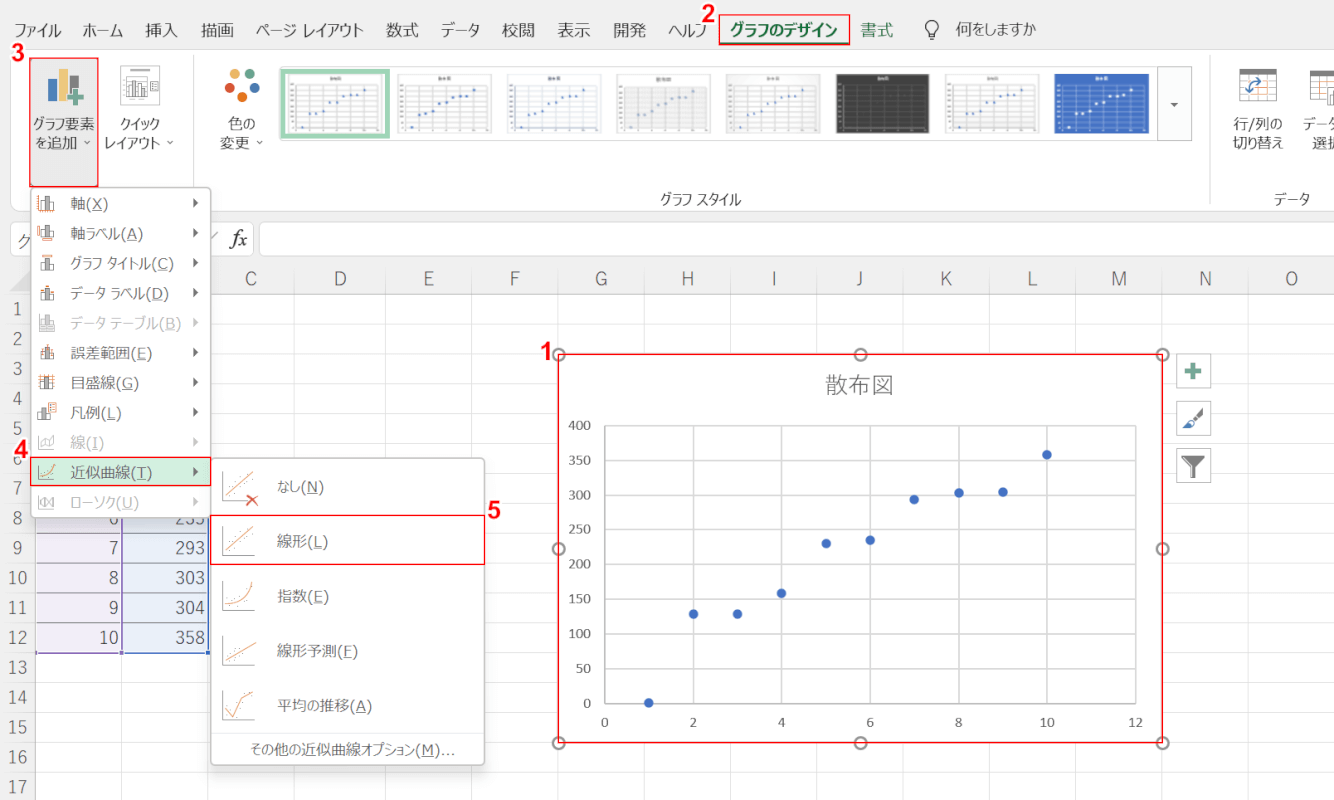
上の画像のような散布図を準備します。①【グラフ】、②【グラフのデザイン】タブの順に選択します。③【グラフ要素を追加】、④【近似曲線】、⑤【任意の種類(例:線形)】の順に選択します。
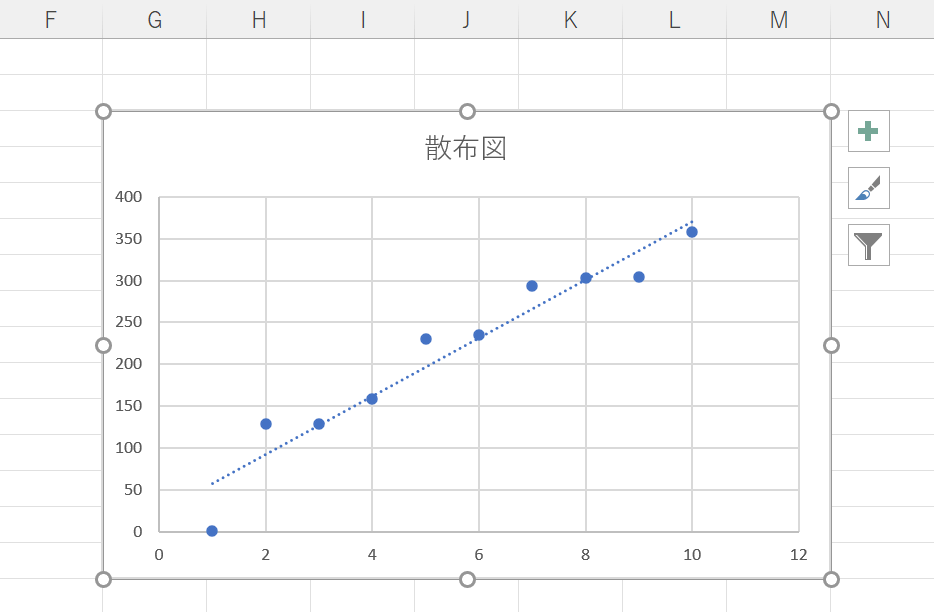
これで、散布図に近似曲線が表示されます。
近似曲線で未来を予測
近似曲線を使って未来のデータを予測する方法をご紹介します。
今回は、1月から6月までの売上金額のグラフを使って7月と8月の売上金額を予測する方法を例に挙げます。
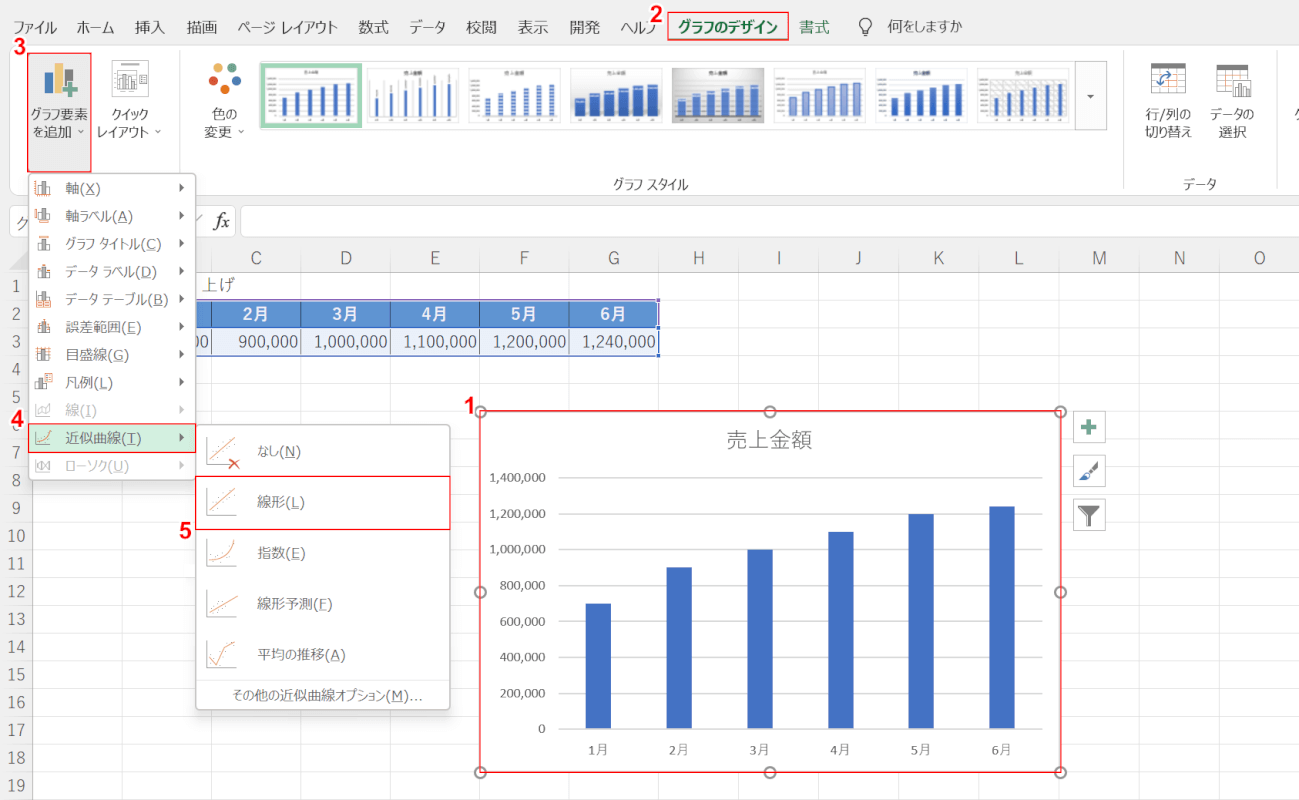
まずは売上金額グラフを、任意の種類のグラフで作成しておきましょう。
①【グラフ】、②【グラフのデザイン】タブの順に選択します。
③【グラフ要素を追加】、④【近似曲線】、⑤【任意の種類(例:線形)】の順に選択します。
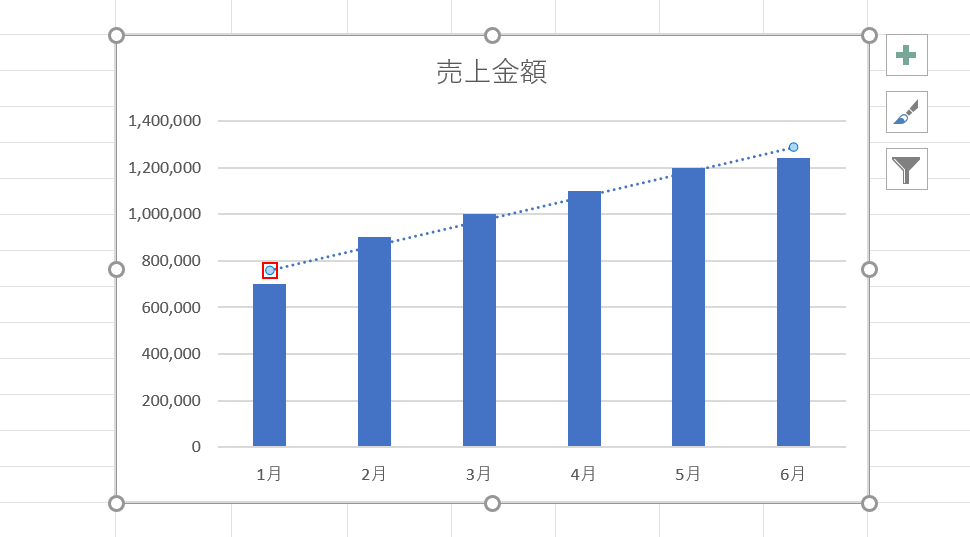
これで、グラフに近似曲線が追加されました。
「近似曲線」を【ダブルクリック】します。

画面右端に「近似曲線の書式設定」画面が表示されます。
①【近時曲線のオプション】を選択します。
「予測」の「前方補外」に任意の数字を入れると、その月数分の予測をすることが出来ます。
②今回は7月と8月の予測がしたいので「2か月分」という意味で『2』と入力し、Enterを押します。
③「グラフに数式を表示する」に【チェックマーク】を入れます。
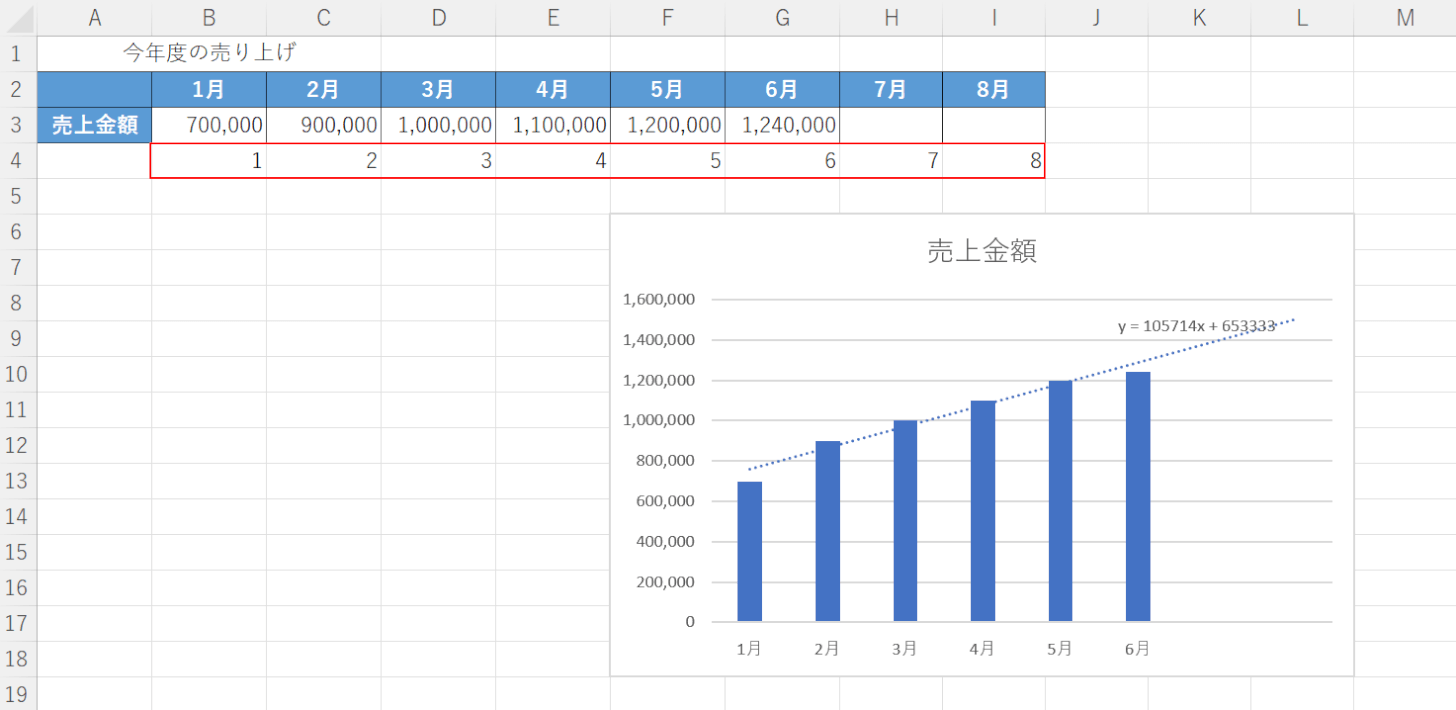
グラフに「y = 105714x + 653333」という数式が表示されました。
今回の「x」は月、「y」は売上金額を表しているので、「x」に月数を代入することで売上金額の予測ができます。
計算をする前に、【表外の任意のセル(例:B4セルからI4セル)】を選択し、予測したい月までの『月数(例:1から8)』を入力しておきましょう。
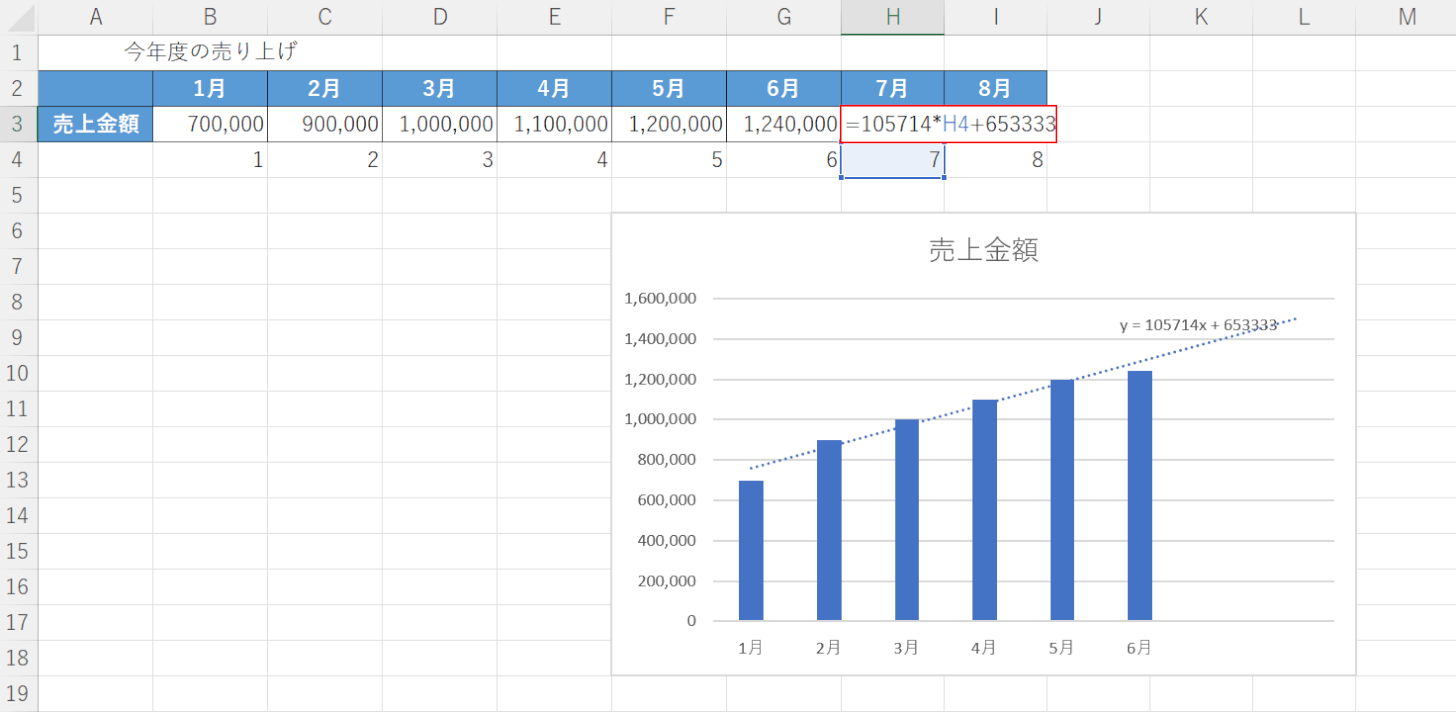
次に、式を入力します。
「y = 105714x + 653333」の「=」以降に月数を代入して入力します。
【7月分の予測を表示したいセル(例:H3セル)】に『=105714*H4+653333』と入力し、Enterを押します。
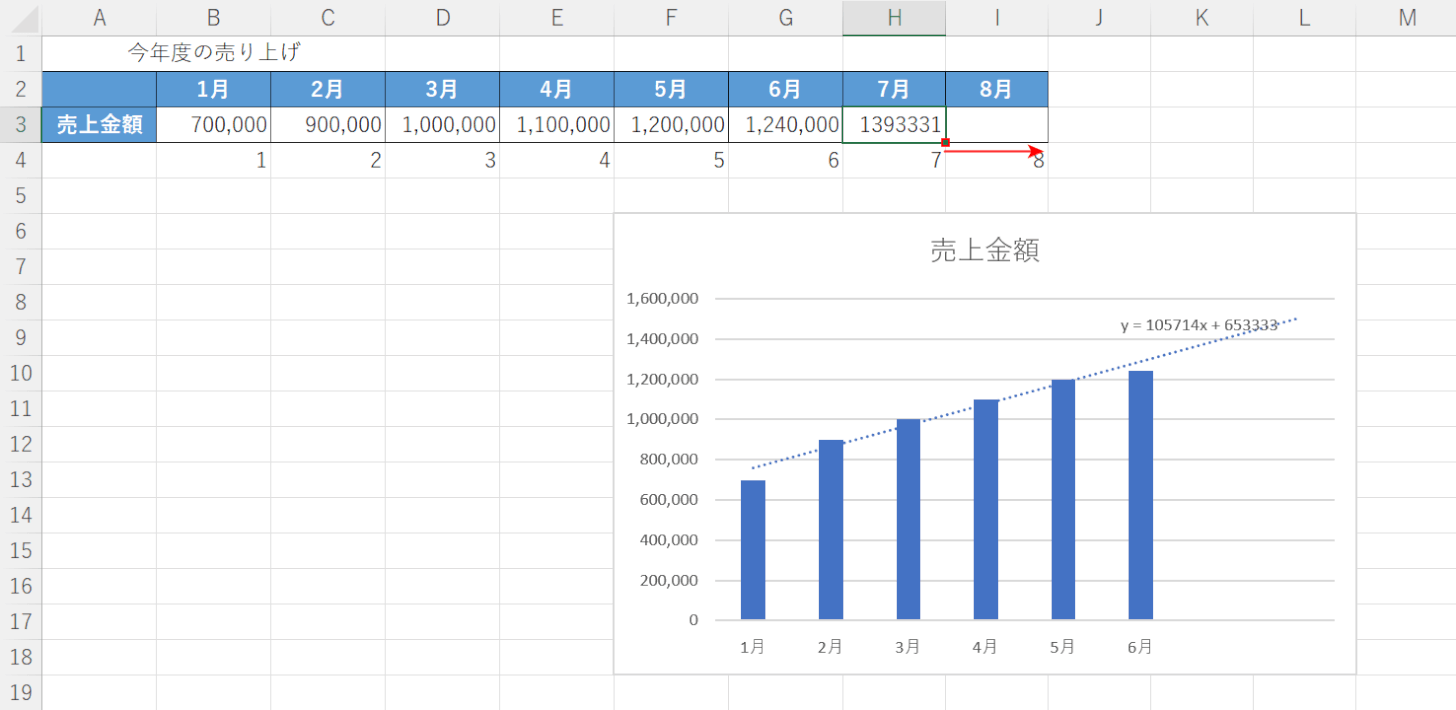
式が完成したら、オートフィルでコピーします。
【関数が入ったセル(例:H3)】を選択し、セルの右下にある「■(フィルハンドル)」を右方向へ【ドラッグ】します。
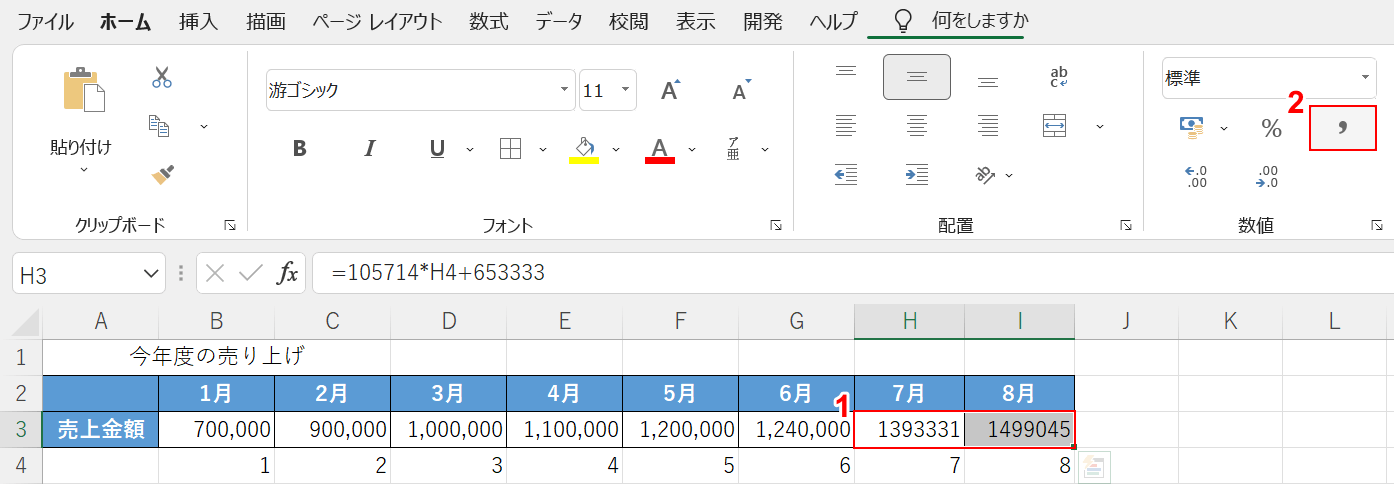
見やすいように、桁区切りスタイルを適用させましょう。
①【対象のセル範囲(例:H3セルからI3セル)】、②【桁区切りスタイル】の順に選択します。
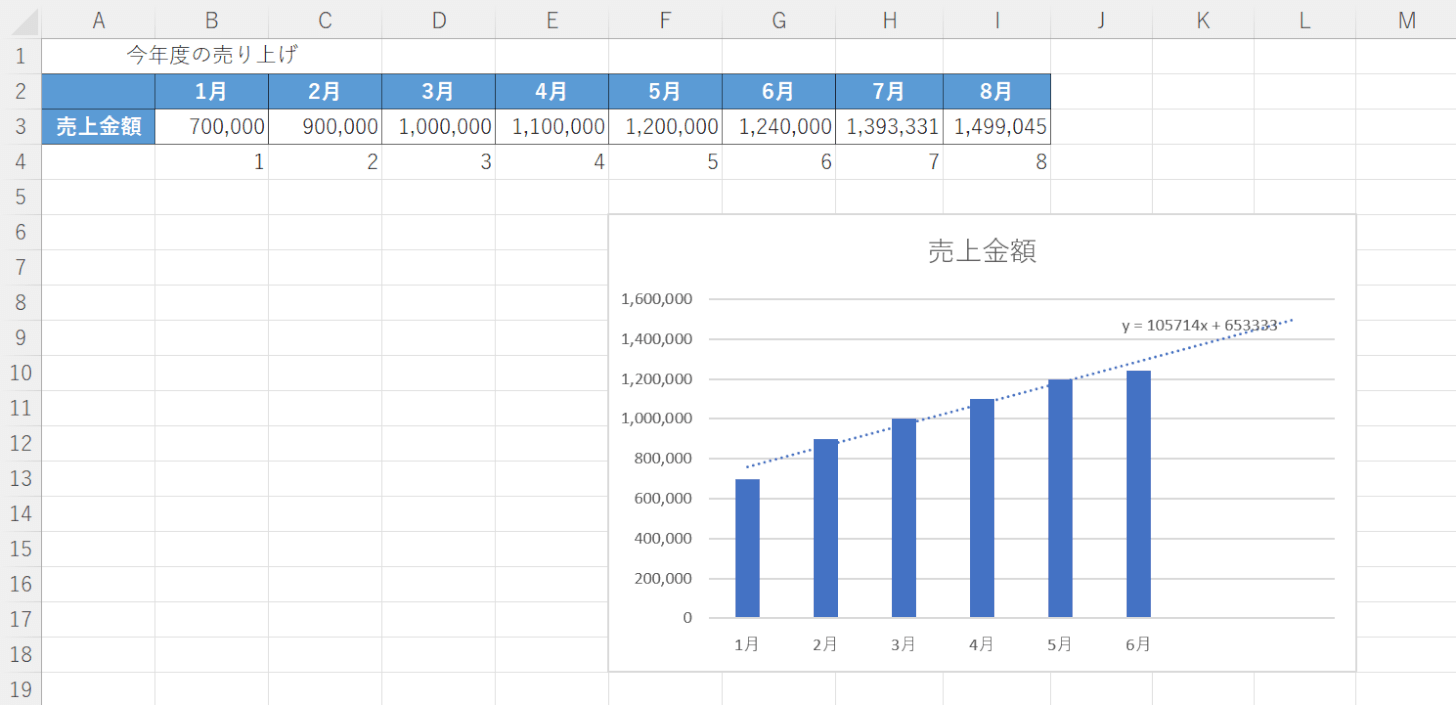
これで、1月から6月までの売上金額を利用して、7月と8月の売上の予測をすることが出来ました。
数式から傾きを求める
数式から傾きを求める方法は以下の通りです。
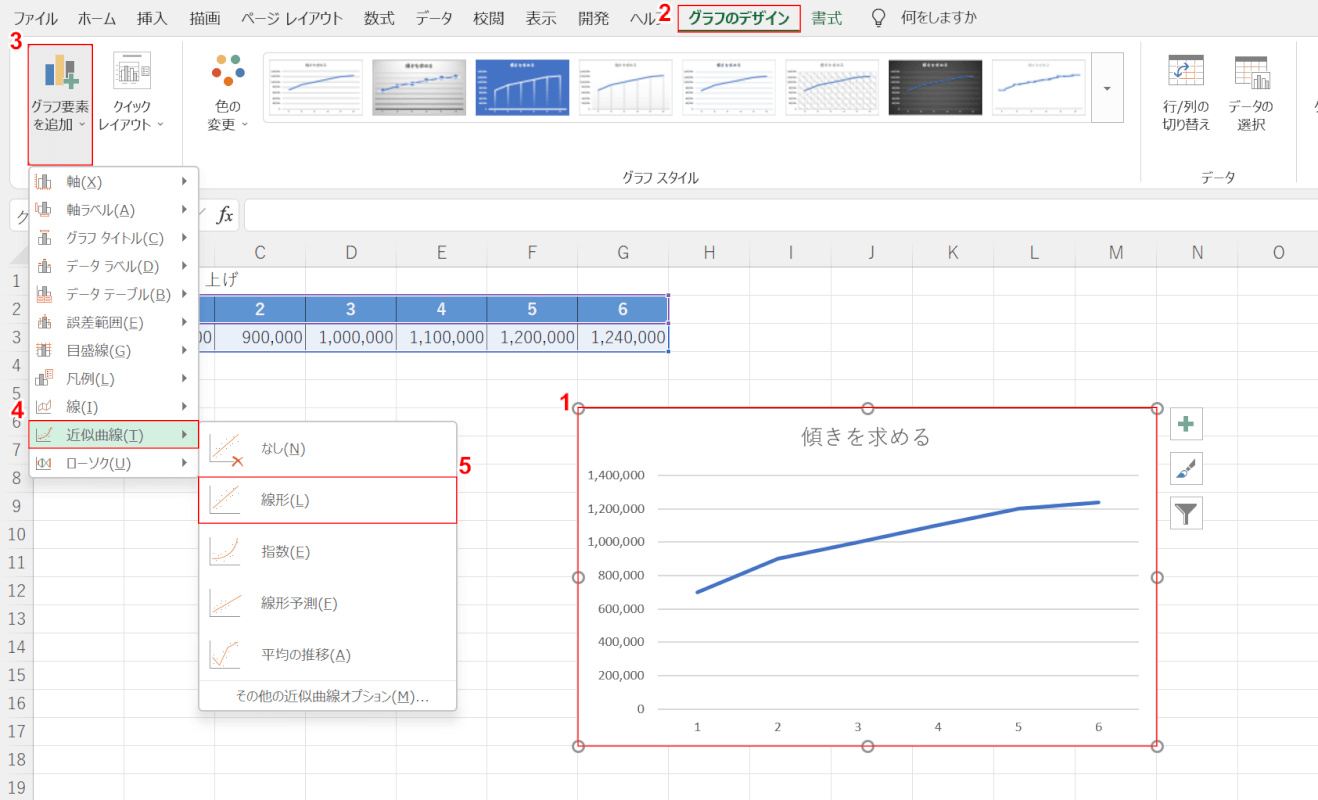
任意のグラフを準備します。
①【グラフ】、②【グラフのデザイン】タブの順に選択します。
③【グラフ要素を追加】、④【近似曲線】、⑤【線形】の順に選択します。
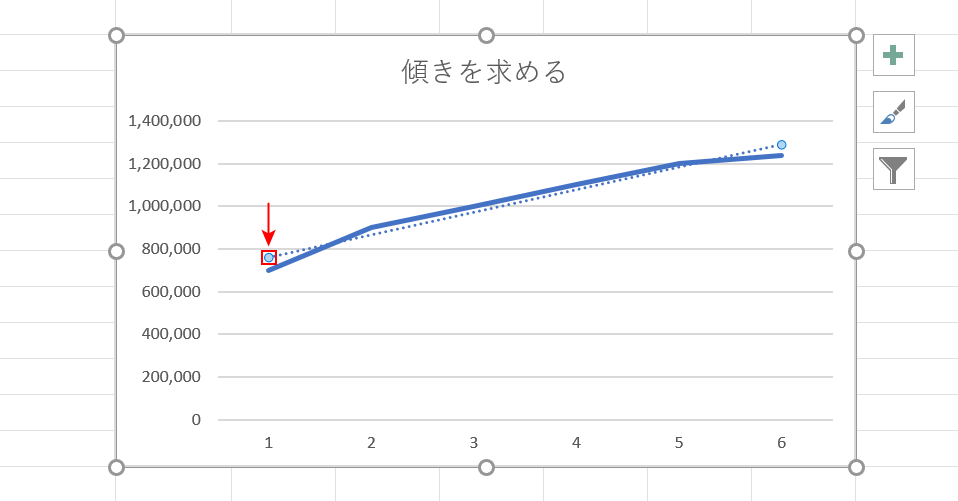
グラフに近似曲線が追加されました。
「近似曲線」を【ダブルクリック】します。

画面右端に「近似曲線の書式設定」画面が表示されます。
①【近似曲線のオプション】を選択し、②「グラフに数式を表示する」に【チェックマーク】を入れます。
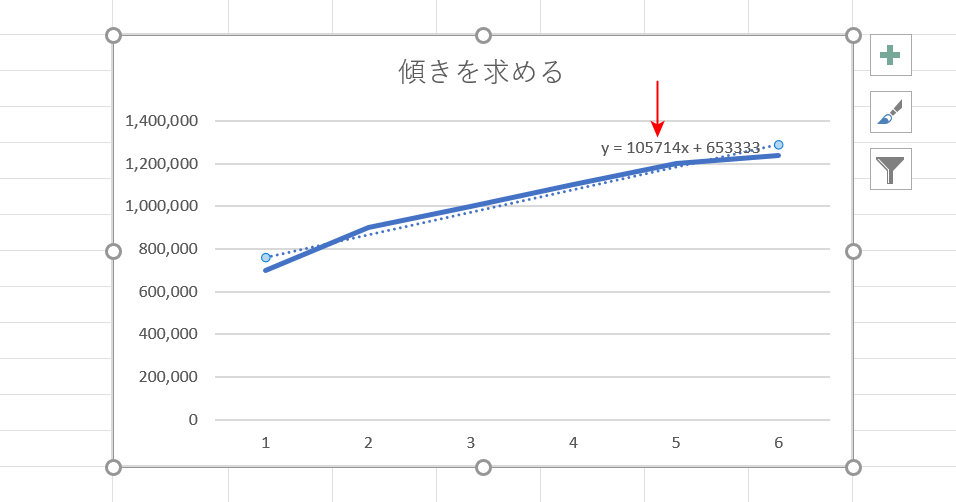
グラフに「y=ax+b」の一次方程式が表示されました。
「a」に入っている値が「傾き」になるので、今回は「105714」が答えになります。
これで数式から傾きを求めることが出来ました。
近似曲線を伸ばす方法
近似曲線を任意の方向に延長する方法をご説明します。
今回は近似曲線を後方に伸ばす方法を例に挙げます。
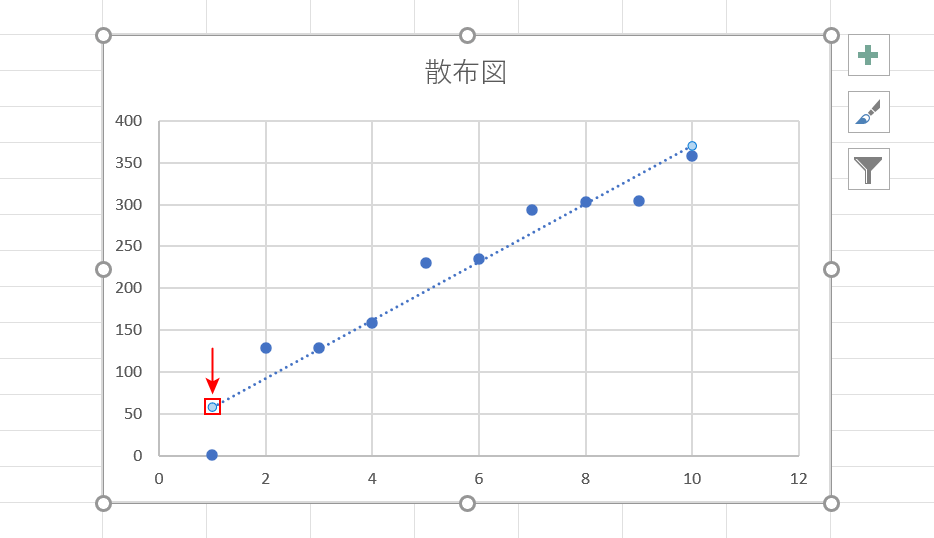
近似曲線を追加したグラフを準備します。
「近似曲線」を【ダブルクリック】します。

画面右端に「近似曲線の書式設定」画面が表示されます。
①【近似曲線のオプション】を選択し、②「予測」の「後方補外」に『任意の数(例:3)』を入力しEnterを押します。
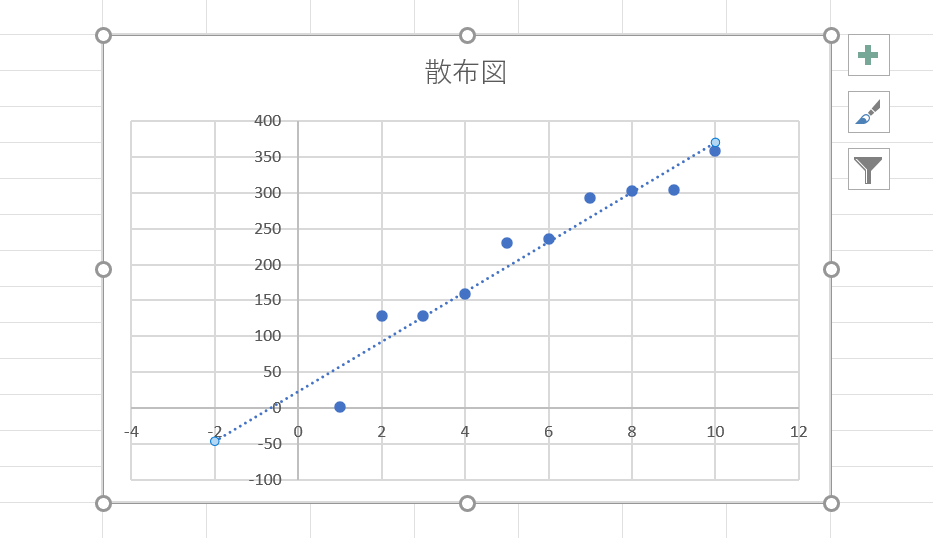
これで、近似曲線を延長することができました。
近似曲線の2本の交点を求める
近似曲線の2本の交点は、数式を連立方程式として解けば求めることが出来ます。
方法は以下の通りです。
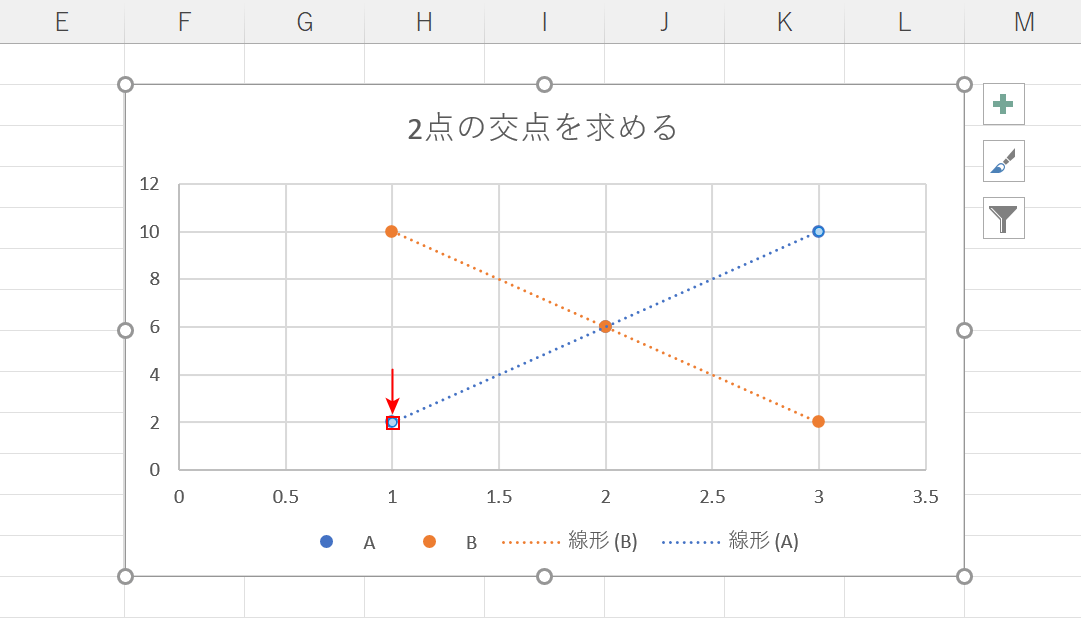
今回は上の画像のようなグラフを例に挙げて2点の交点を求めます。
まずはそれぞれの数式を表示させましょう。
「近似曲線」を【ダブルクリック】します。

画面右端に「近似曲線の書式設定」画面が表示されます。
①【近似曲線のオプション】を選択し、②「グラフに数式を表示する」に【チェックマーク】を入れます。
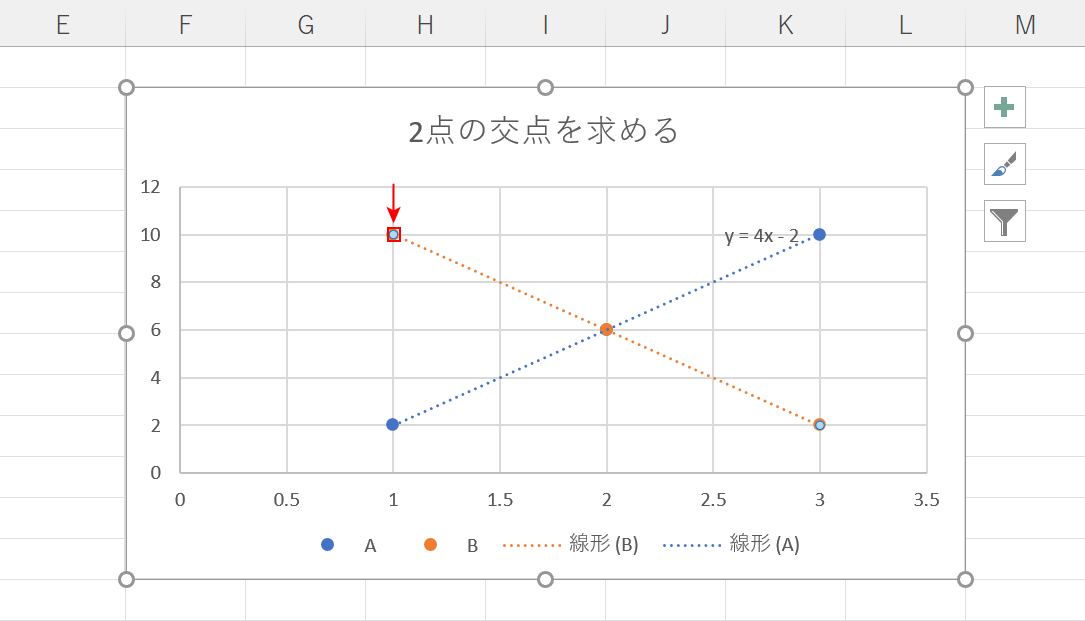
グラフに戻ります。
「もう一方の近似曲線」を【ダブルクリック】します。

画面右端に「近似曲線の書式設定」画面が表示されます。
①【近似曲線のオプション】を選択し、②「グラフに数式を表示する」に【チェックマーク】を入れます。
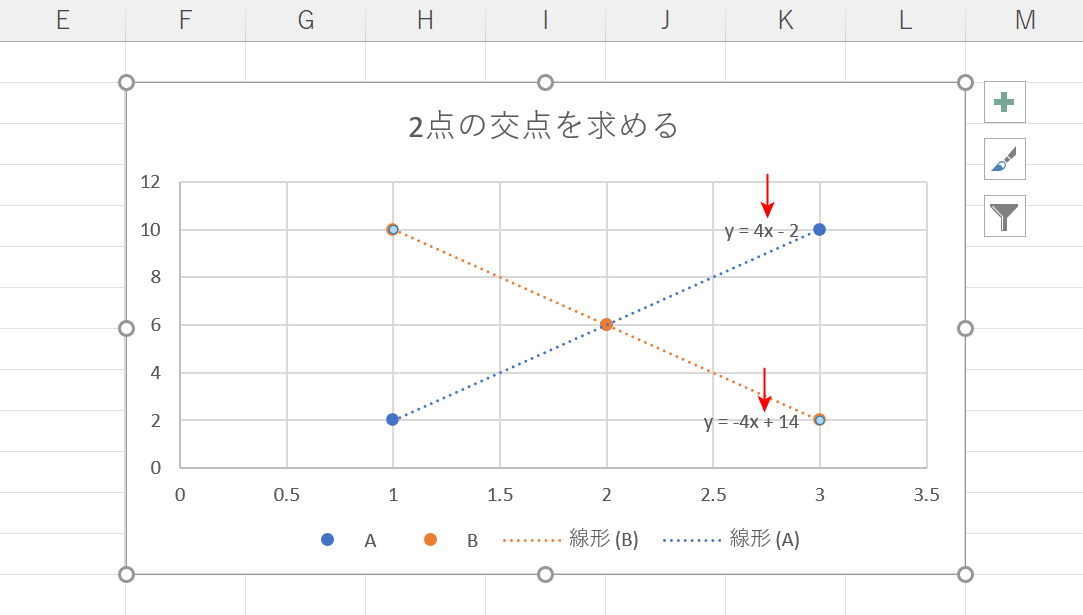
これで、赤い矢印で示したように2つの近似曲線の数式が表示されました。
この2つの数式を連立方程式として解きます。
以下は代入法で解を求めた例です。
Aの近似曲線がy=4x-2 Bの近似曲線がy=-4x+14 AをBに代入してxの値を求めます。 (4x-2)=-4x+14 4x-2=-4x+14 4x+4x=14+2 8x=16 x=2 次にx=2をAの数式に代入して、yの値を求めます。 y=(4×2)-2 y=8-2 y=6 x=2、y=6が求められたので (x,y)=(2,6)
これで、近似曲線の交点を求めることができました。
近似曲線が追加できない場合
近似曲線は以下のグラフでは追加できません。
対象のグラフが以下のグラフにあてはまる場合は、データやグラフを見直して再度作成し直しましょう。
- 積み上げ縦棒グラフ
- 積み上げ横棒グラフ
- 円グラフ
- ドーナツグラフ
- 箱ひげ図
