エクセルでのカイ二乗検定のやり方

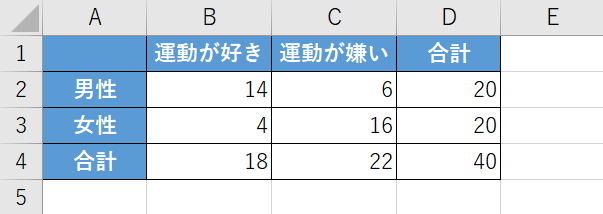
例えば男女別に「運動が好きか嫌いか」のアンケートを取り、上の画像の表のような結果が得られたとします。

表を見ると、一見「男性は"運動が好き"」「女性は"運動が嫌い"」と読み取れるので「運動が好きか嫌いかは、男女によって差が出る」という結果が得られそうです。しかし、偶然この結果が得られただけという可能性もあるためデータだけで判断することは出来ません。

こういった場合にカイ二乗検定を使って、「データ同士には関係があるのかどうか」を調べます。

上の画像の例にあてはめると、カイ二乗検定を使うことで「性別によって運動の好き嫌いに差が出るのかどうか」を調べられるということになります。

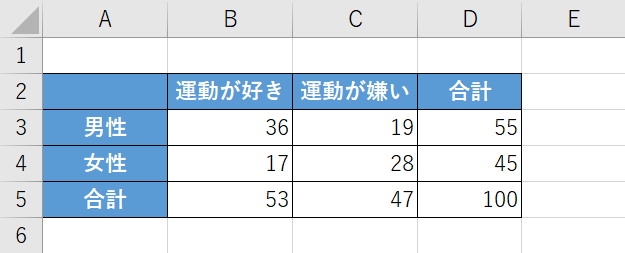
カイ二乗検定は、2つのデータ群の結果に差があるかどうかを調べることが出来る検定方法です。

上の画像の場合、2つのデータ群とは「回答者が男性か女性か」と「運動が好きか嫌いか」という2つの質問から得られたデータということになります。

カイ二乗検定を行う場合、2つのデータ群については必ず上の画像のようにクロス集計表としてまとめておきましょう。

クロス集計とはアンケート結果を「男女別」「年代別」など属性ごとに分けたり、異なる質問を掛け合わせたりして集計する方法です。

以下の記事では、クロス集計のやり方やクロス集計の種類等についてご説明していますので参考にしてみて下さい。

エクセルのクロス集計のやり方をわかりやすく説明

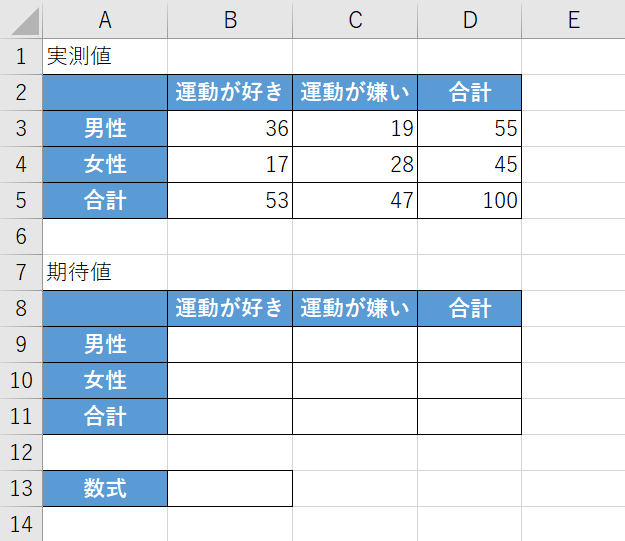
今回は男女別に「運動が好きか嫌いか」のアンケートを取り上の画像の表のような結果が得られたと仮定して、「運動が好きか嫌いかという結果には性別が関係しているかどうか」を調べます。

カイ二乗検定では、「実測値」と「期待値」を使ってデータの差を計算します。

実測値とは「実際にデータとして得た値（例：アンケート結果）」のことで、期待値とは「"運動が好きか嫌いかに性別は関係ない"場合はこれくらいの値になるだろう」と推測される値のことを指します。

「実際のデータ」と「運動が好きか嫌いかに性別は関係ないという結果が得られた場合の値」に大きな差があれば「関係がある」、差がなければ「関係がない」と判断します。

上の画像のように、クロス集計表と同じ表を期待値を求めるための表としてコピーしておきましょう。

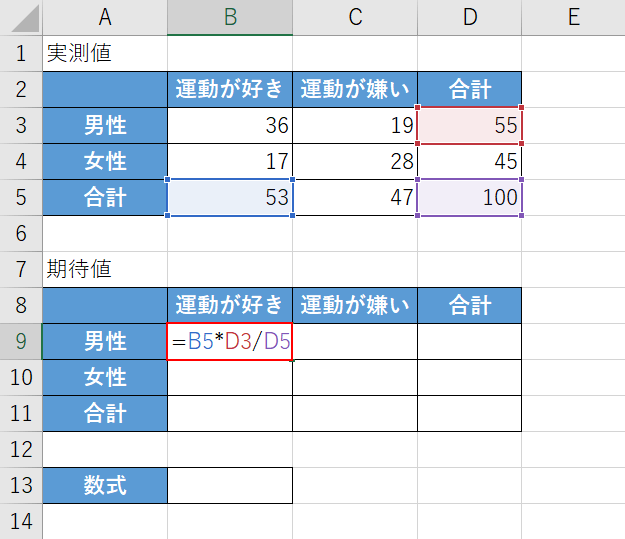
まずは、それぞれの結果の期待値を求めていきます。

期待値は、全ての結果の割合が同じであると仮定して求めます。

【任意のセル（例：B9セル）】を選択して、『=B5*D3/D5』と入力し、Enterを押します。

【任意のセル（例：C9セル）】を選択して、『=C5*D3/D5』と入力し、Enterを押します。

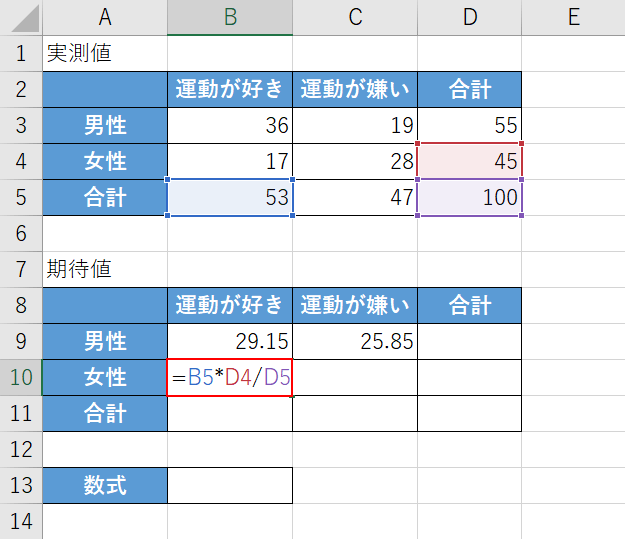
【任意のセル（例：B10セル）】を選択して、『=B5*D4/D5』と入力し、Enterを押します。

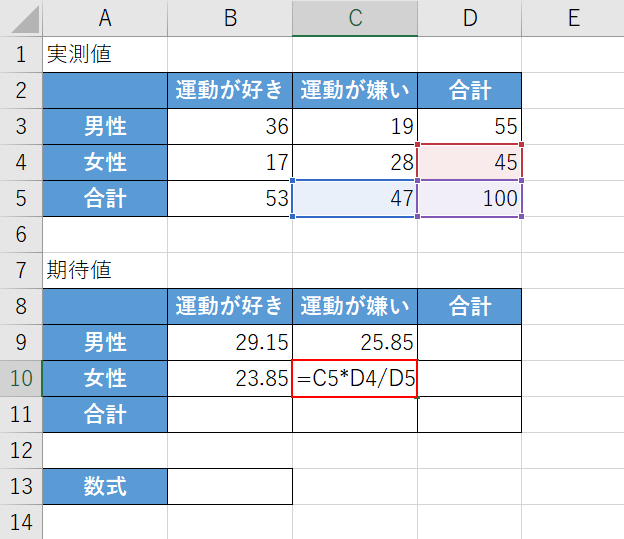
【任意のセル（例：C10セル）】を選択して、『=C5*D4/D5』と入力し、Enterを押します。

すべての期待値を入力し終わったら、任意で合計も出しておきましょう。

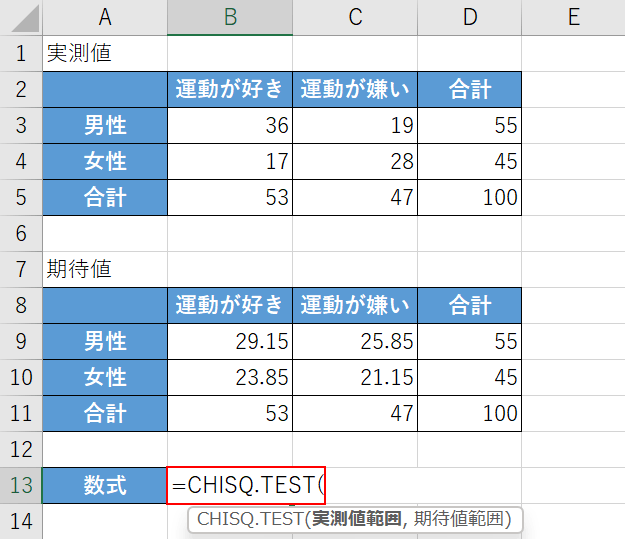
次に「帰無仮説」と「対立仮説」を立てて、「帰無仮説が起こる確率」を関数で求めます。

今回の場合、帰無仮説は「実測値と期待値に"差がない"と仮定すること」を指し、対立仮説は「実測値と期待値に"差がある"と仮定すること」を指します。

「差がある」ことを調べたい場合は膨大なパターンの計算をしなければなりませんが、「差がない」という結果は1つだけなので計算することが出来ます。

帰無仮説が起こる確率はCHISQ.TEST（カイ・テスト）関数を使って求めることが出来ます。

CHISQ.TEST関数の書式は、「=CHISQ.TEST(実測値範囲,期待値範囲)」です。

まずは【任意のセル（例：B13セル）】を選択して、『=CHISQ.TEST(』と入力します。

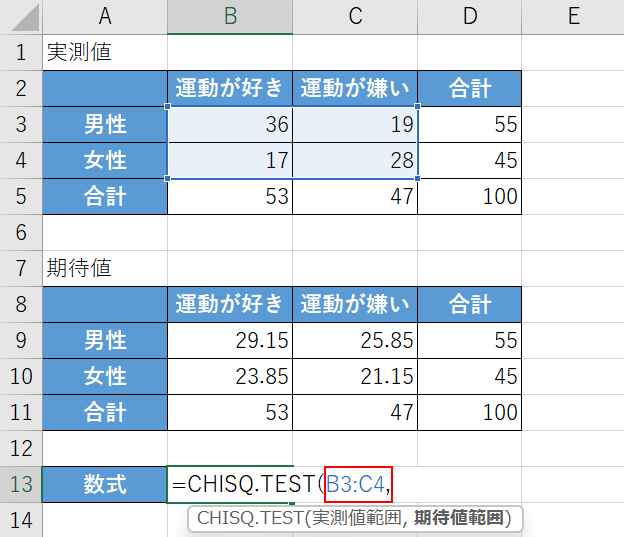
次に、実測値範囲の引数を設定します。

「=CHISQ.TEST(」に続いて『B3:C4,』と入力します。

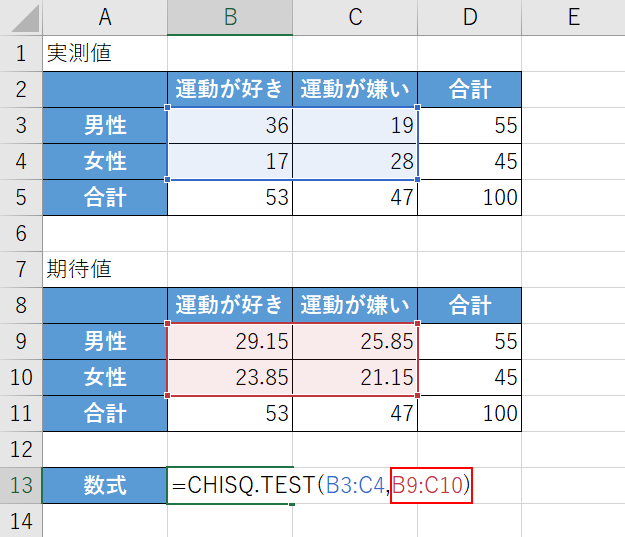
「=CHISQ.TEST(」に続いて『B9:C10)』と入力し、Enterを押します。

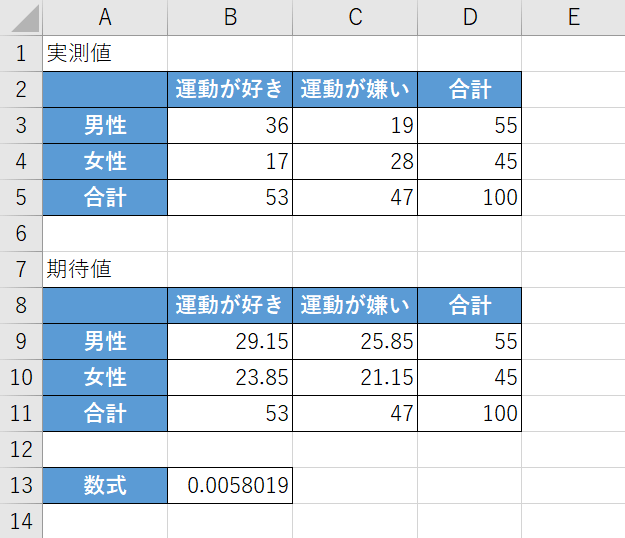
「0.0058019」という結果が出ました。

一般的に0.05以下であれば、帰無仮説で仮定した事象はめったに起こらないとされています。

今回は、結果が0.05以下であるため「運動が好きか嫌いかという結果には性別が関係していない」という事象が現れる確率は低いとなり、今回の架空のアンケート結果からの結論としては「運動が好きか嫌いかという結果には性別が関係していると判断できる」ということになります。