- 公開日:
エクセルでの正規分布グラフの作り方
この記事では、エクセルでの正規分布グラフの作り方をご紹介します。
「正規分布」とは、統計でデータ分析をするにあたっての基礎的な考え方です。
以下では、正規分布についての基本的な知識や、正規分布に関するエクセルの関数等についてご紹介しています。
正規分布とは?
まず、正規分布についてご説明します。
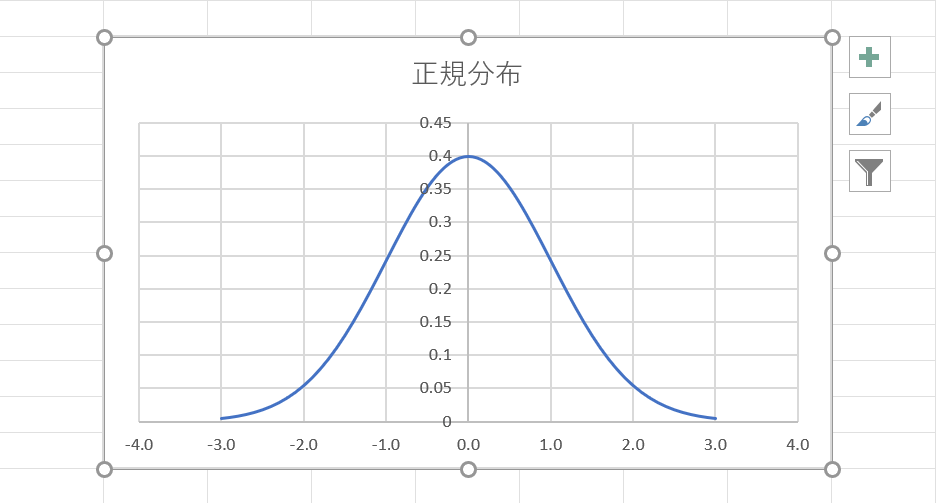
正規分布とは、「統計」の基礎的な考え方です。
簡単に説明すると「世の中の多くの現象が現れる確率を計算すると、平均値が一番確率が高く平均から離れるにつれて確率が下がっていく」という考え方になります。
上の画像はエクセルで正規分布グラフを作った例です。
多くの統計分布や確率の分布は、この釣鐘型のグラフの形に近づきます。
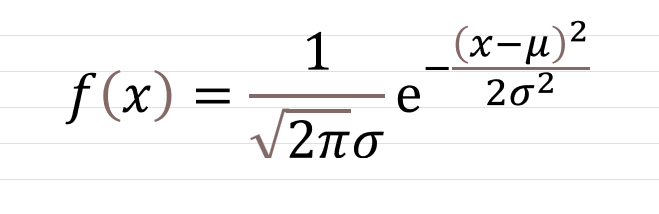
上の画像は「確率密度関数(対象の現象がxになる確率を示した関数)」の数式で、この数式が正規分布を示す数式になります。
上記の数式を使うと「平均値」と「標準偏差」が分かれば「対象の現象がxになる確率を示した関数=確率密度関数」を導き出すことが出来ます。
今回は、この数式と同じ働きをするエクセルの関数として「NORM.DIST(ノーマル・ディストリビューション)関数」をご紹介します。
標準偏差の求め方については以下の記事をご参照ください。
エクセルのNORM.DIST関数について
あらかじめ「平均値」と「標準偏差」が分かっていれば、NORM.DIST関数を使って「あるデータがxの値になる確率を示した関数」を導き出すことが出来ます。
NORM.DIST関数の書式は、「=NORM.DIST(x,平均,標準偏差,関数形式)」です。
引数を以下の表にまとめましたので参考にしてみて下さい。
| 引数 | 引数の意味 |
|---|---|
| X | 正規分布関数に代入する値を指定します。 必須。 |
| 平均 | 対象となる分布の算術平均を指定します。 必須。 |
| 標準偏差 | 対象となる分布の標準偏差を指定します。 必須。 |
| 関数形式 | 関数の形式を論理値で指定します。 TRUEの場合は「累積分布関数」、FALSEの場合は「確率密度関数」を返します。 必須。 |
NORM.DIST関数の使い方の例
NORM.DIST関数を使って「あるグループの女性の平均身長が157cm、標準偏差が3.0cmの場合150cm以下の女性はグループ全体にどれくらいの割合いるのか」という計算をしてみます。
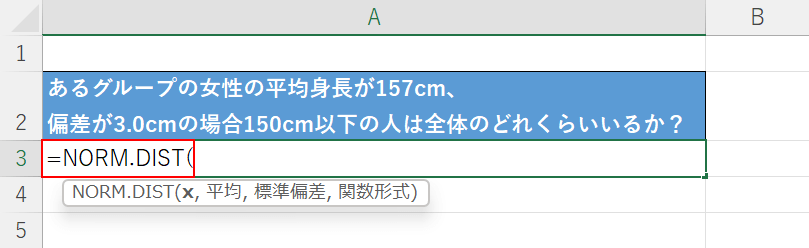
まず、「NORM.DIST関数」を入力します。
【任意のセル(例:A3セル)】を選択し、『=NORM.DIST(』と入力します。
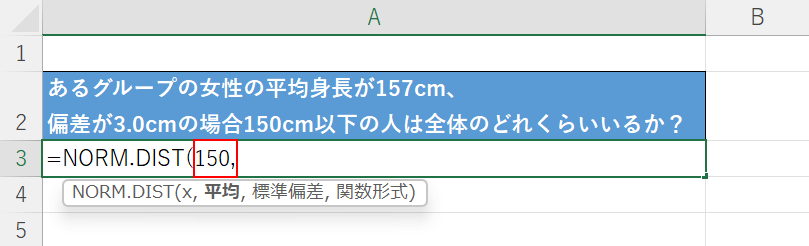
次にxの引数を設定します。
今回は150cm以下の割合が知りたいので、「=NORM.DIST(」に続いて『150,』と入力します。
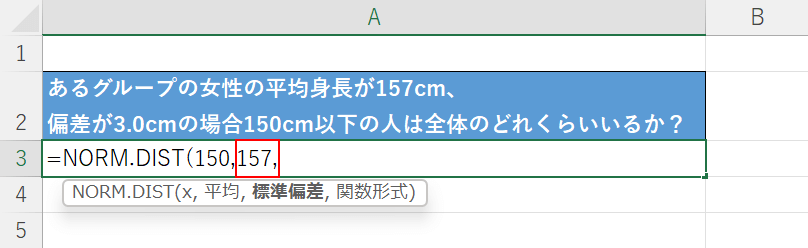
次に、平均の引数を設定します。
今回は「平均身長が157cm」のグループから割合を導き出すので、「150,」に続いて『157,』と入力します。
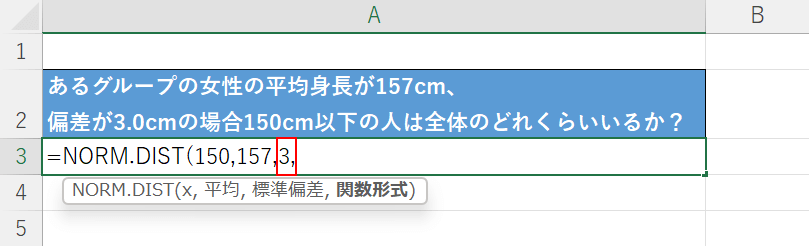
次に、標準偏差の引数を設定します。
今回は、「3.0cm」が標準偏差になるため「157,」に続いて『3,』と入力します。

次に関数形式を選択します。
今回は「確率密度関数」を求めたいので『FALSE)』と入力し、Enterを押します。
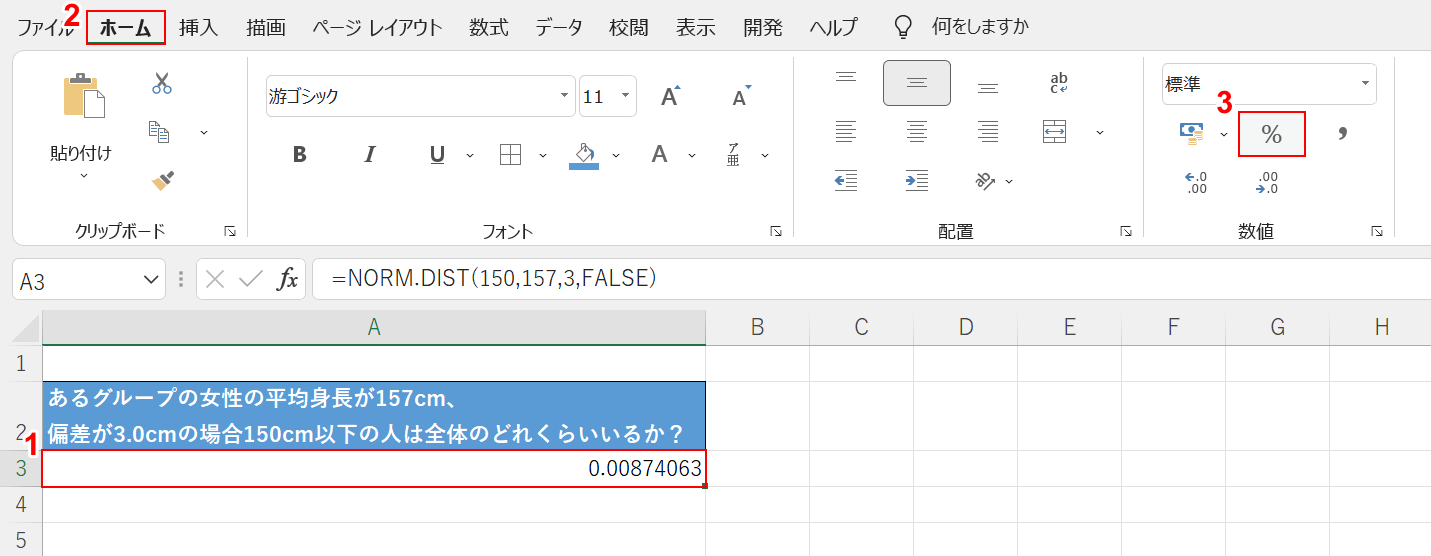
結果が表示されました。
次に値を見やすい形式に編集します。
①【NORM.DIST関数を入力したセル(例:A3セル)】、②【ホーム】タブ、③【パーセント スタイル】の順に選択します。
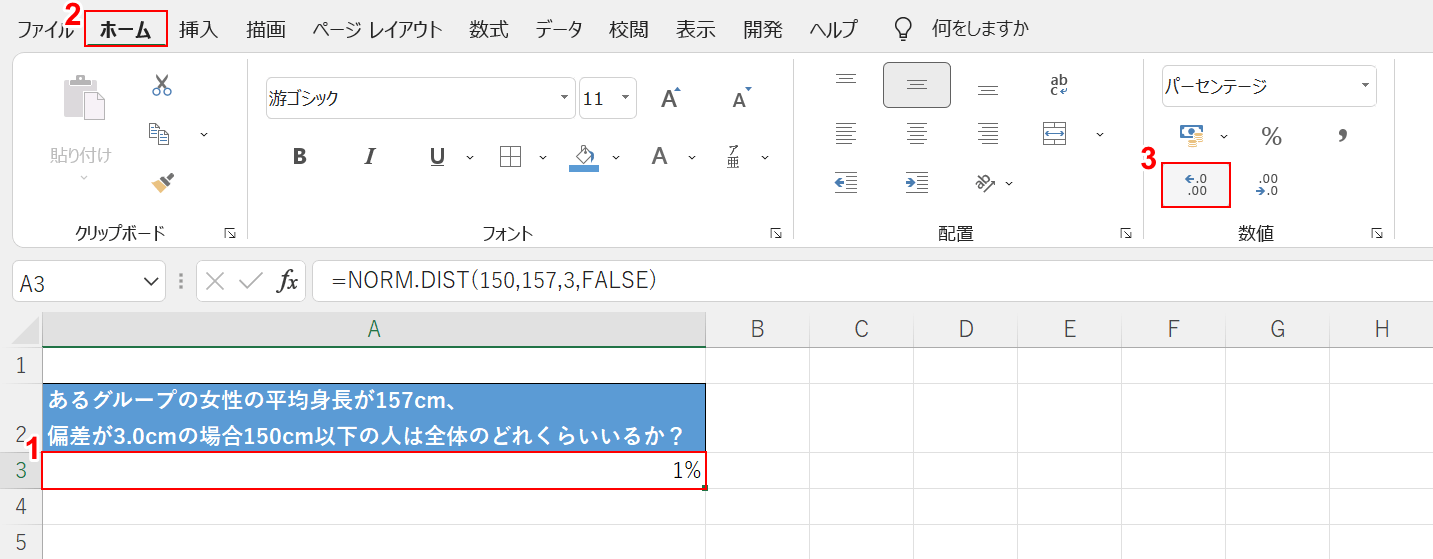
値が四捨五入されてしまうので、小数点以下の桁数を調整します。
①【NORM.DIST関数を入力したセル(例:A3セル)】、②【ホーム】タブの順に選択し、③【パーセント スタイル】を2回選択します。

これで、NORM.DIST関数を使って「あるグループの女性の平均身長が157cm、標準偏差が3.0cmの場合150cm以下の人の割合」を求めることが出来ました。
正規分布曲線グラフの作り方
NORM.DIST関数を使った正規分布曲線グラフの作り方をご紹介します。

今回は上の画像のように、A列に入力した「1」から「10」の値を使って正規分布グラフを作成していきます。
「平均」は、D2セルにAVERAGE関数を使ってA2セルからA11セルの平均を出しています。
AVERAGE関数の書式や、基本的な使い方等については以下の記事でご紹介しています。
次に、標準偏差をエクセルの「STDEV.P関数」で求めます。
「STDEV.P関数」の書式は「=STDEV.P(数値1,[数値2],…)」です。
【任意のセル(例:E2セル)】を選択し、『=STDEV.P(』と入力します。
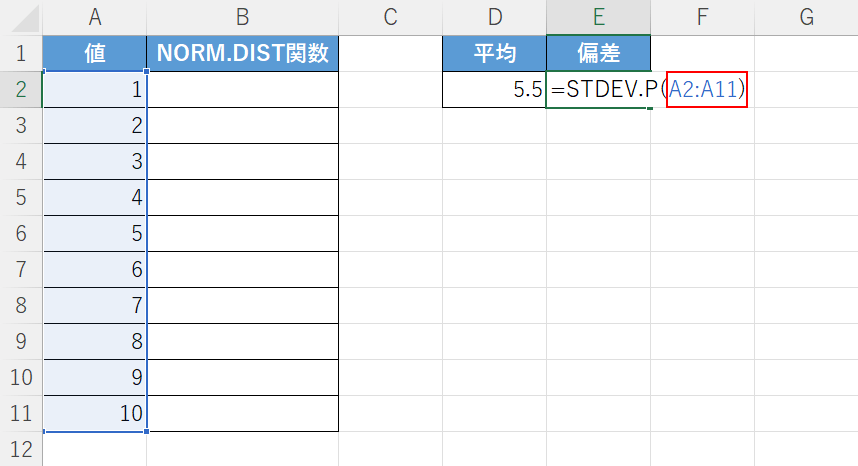
A2セルからA11セルに入力された「1」から「10」の値の標準偏差を求めるので、「=STDEV.P(」に続き『A2:A11)』と入力し、Enterを押します。
これで、NORM.DIST関数を使って正規分布グラフを作成する準備が出来ました。
次にNORM.DIST関数を入力します。
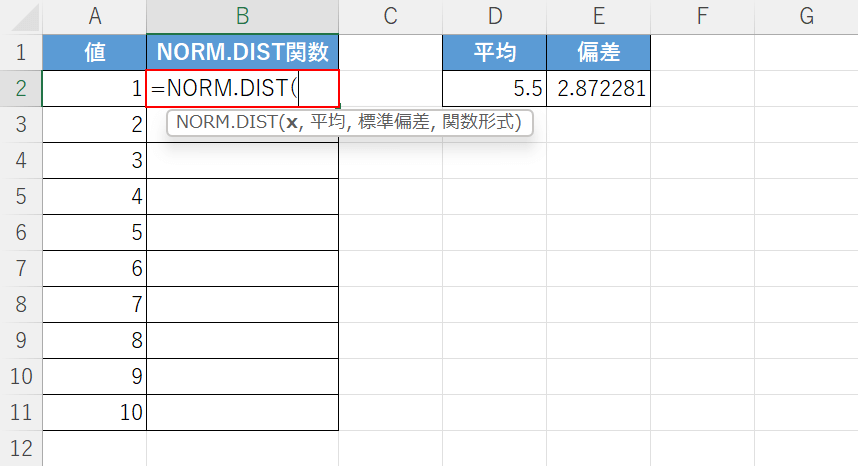
【任意のセル(例:B2セル)】を選択し、『=NORM.DIST(』と入力します。
次に、NORMDIST関数のxの引数を設定します。
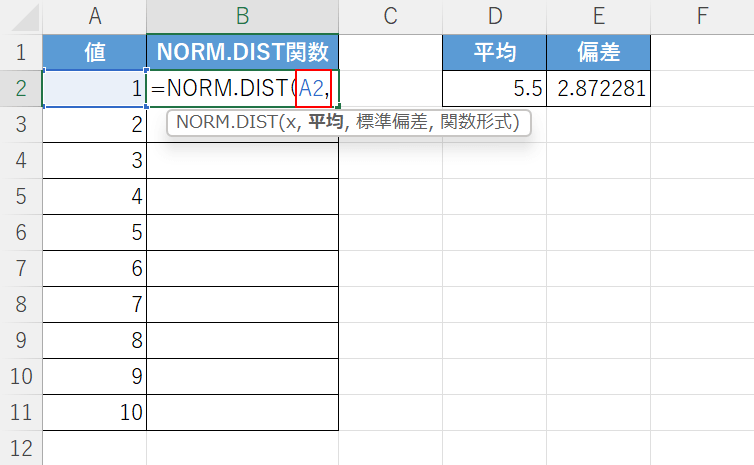
今回はA列に入力されたデータを使うので「=NORM.DIST(」に続いて『A2,』と入力します。
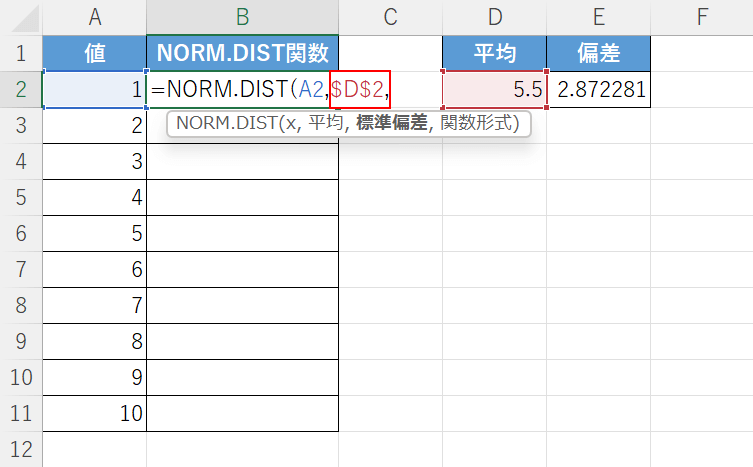
次に、平均の引数を設定します。
D2セルに平均値が入力されているので、「A2,」に続いて『$D$2,』と入力します。
後ほどオートフィルで式をコピーするので、絶対参照をつけておきましょう。
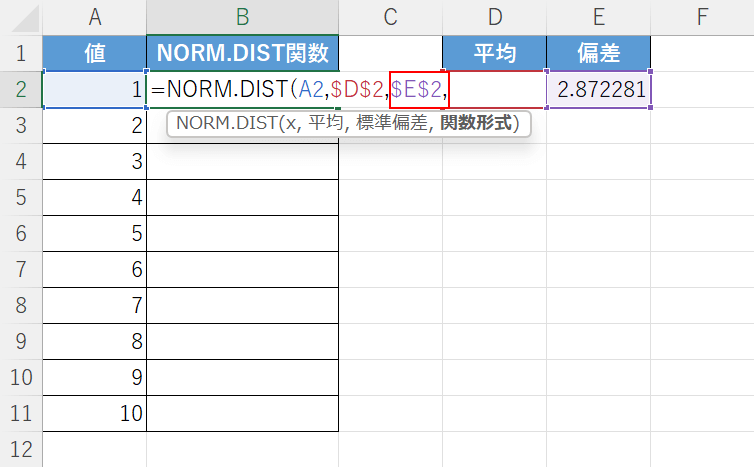
次に、標準偏差の引数を設定します。
先ほどSTDEV.P関数で標準偏差を求めたE2セルを指定します。
「D$2$,」に続いて『$E$2,』と入力します。
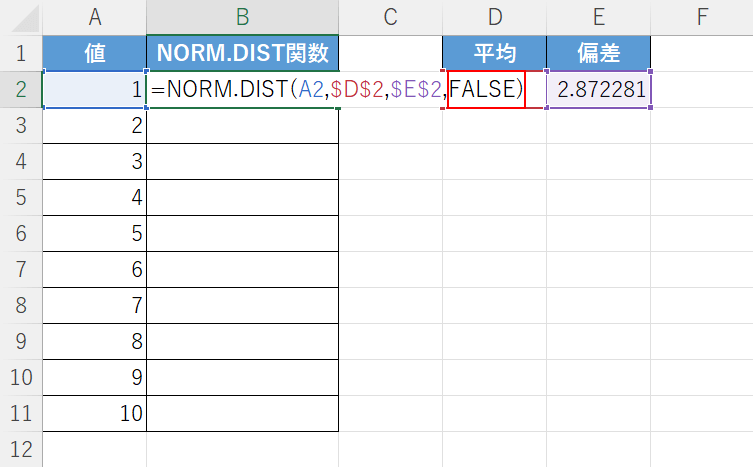
次に、関数形式の引数を設定します。
今回は、「確率密度関数」を求める「FALSE」を設定します。
「$E$2,」に続いて『FALSE)』と入力し、Enterを押します。

式が完成したら、オートフィルでコピーします。
【関数が入ったセル(例:B2)】を選択し、セルの右下にある「■(フィルハンドル)」を下方向へ【ドラッグ】します。
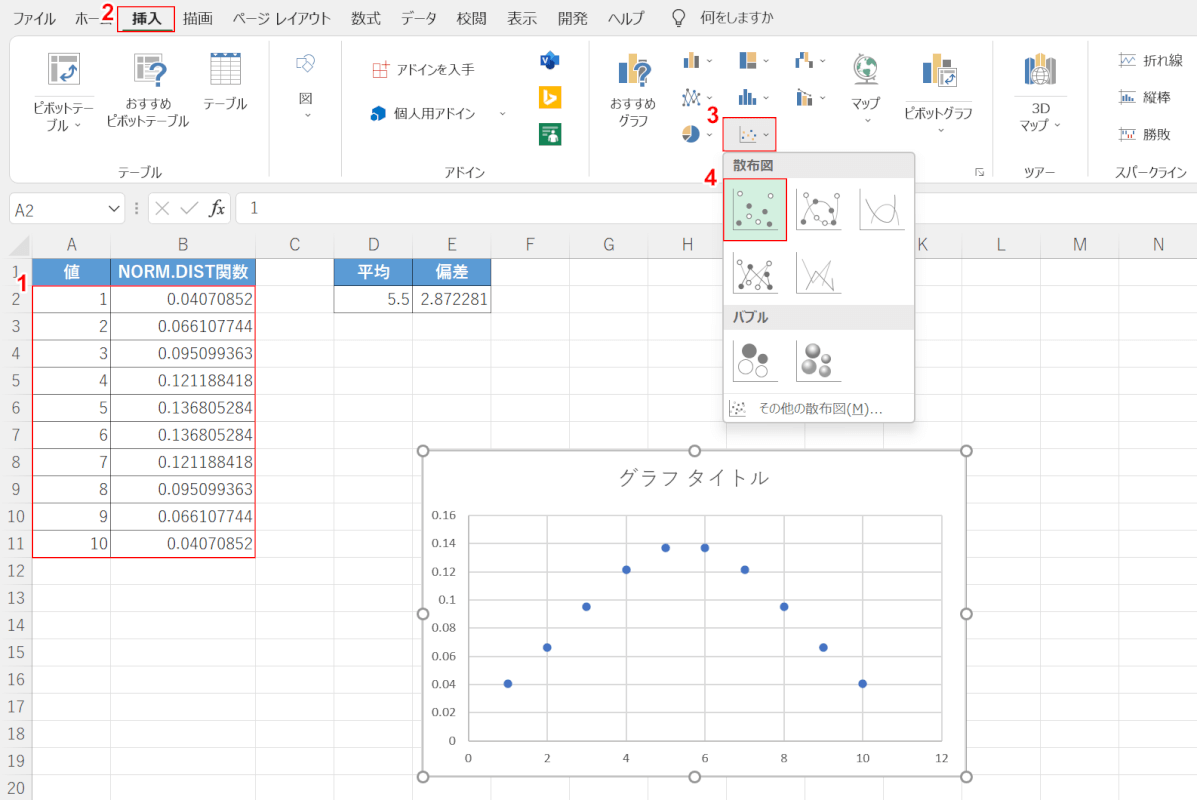
これで、表が完成しました。
表を元に正規分布グラフを作成します。
①【表(例:A2セルからB11セル)】を選択します。
②【挿入】タブ、③【散布図】、④【散布図】の順に選択します。
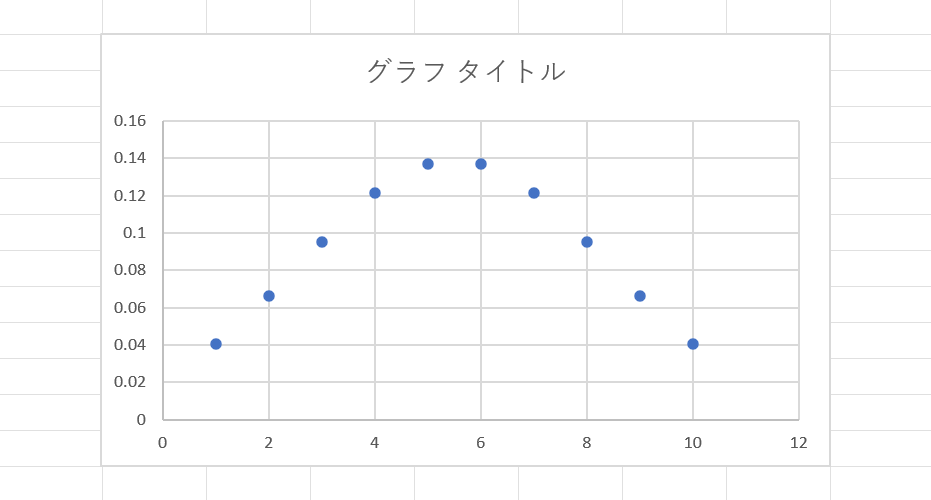
これで、正規分布グラフが完成しました。
データの数を増やすことで、さらに釣鐘型に近いグラフを作成することが出来ます。
