エクセル関数を使った共分散の求め方

この記事では、エクセルの関数を使った共分散の求め方についてご説明します。

共分散とは2つの対応するデータ間に関係があるのかどうかを分析するために求める値です。

エクセルを使えば共分散を簡単に求めることが出来ます。

以下では、共分散が求められる関数の書式や引数等についても詳しくご説明しています。

共分散とは？

共分散とは、2つのデータ同士の関係を表す値です。

例えば、「数学の点数が高い生徒は、物理の点数も高い傾向にあるのか」「気温が高ければ、飲料の売上もあがるのか」といったような対応する2つのデータに関係があるのかどうかを分析できます。

共分散の結果は以下のように解釈されます。

• 共分散が大きい（正の数）場合は、Aが大きいときBも大きい傾向がある
• 共分散が0に近い場合は、AとBの関係は小さい
• 共分散が大きい（負の数）場合は、Aが大きいときBも小さい傾向がある

標本の共分散を求めるCOVARIANCE.S関数とは？

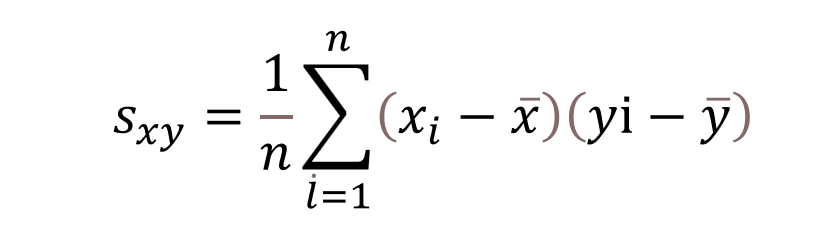
上の画像は、共分散を求める公式です。

共分散の値を調べたい場合は、2つのデータをxとyとし、上記の公式を解きます。

この公式と同じ働きをする関数が、COVARIANCE.S（コバリアンス・エス）関数です。

以下では、COVARIANCE.S関数についての詳細をご紹介します。

COVARIANCE.S関数の用途

COVARIANCE.S関数の用途については、以下のような例があります。

• 身長が高ければ、体重も大きくなるかを調べる時
• 勉強時間が長い生徒ほど、テストの点数が高いのかを調べる時
• 商品Aの売上が高いときは、商品Bの売上も高いのかどうかを調べる時

COVARIANCE.S関数の書式

まずは、COVARIANCE.S関数の書式を確認していきましょう。

COVARIANCE.S関数は、「=COVARIANCE.S(配列1,配列2)」のように記述します。

引数を1つずつ確認していきましょう。

※引数（ひきすう）とは、Excelの関数を使用する際に必要な情報です。関数が結果を返すための判断材料とイメージしましょう。関数名の後の括弧「()」内に入力します。

第1引数（配列1）

1番目の引数は「配列1」です。この引数は必須です。

データが入力されているセル範囲を指定します。

データは整数である必要があります。

第2引数（配列2）

2番目の引数は「配列2」です。この引数は必須です。

データが入力されているもう一方のセル範囲を指定します。

データは整数である必要があります。

COVARIANCE.S関数を使った共分散の求め方

COVARIANCE.S関数を使った共分散の求め方をご紹介します。

今回は、「気温」と「炭酸飲料の売上」のデータを例に挙げて「気温が高い日は炭酸飲料の売上も高いのか」を分析します。

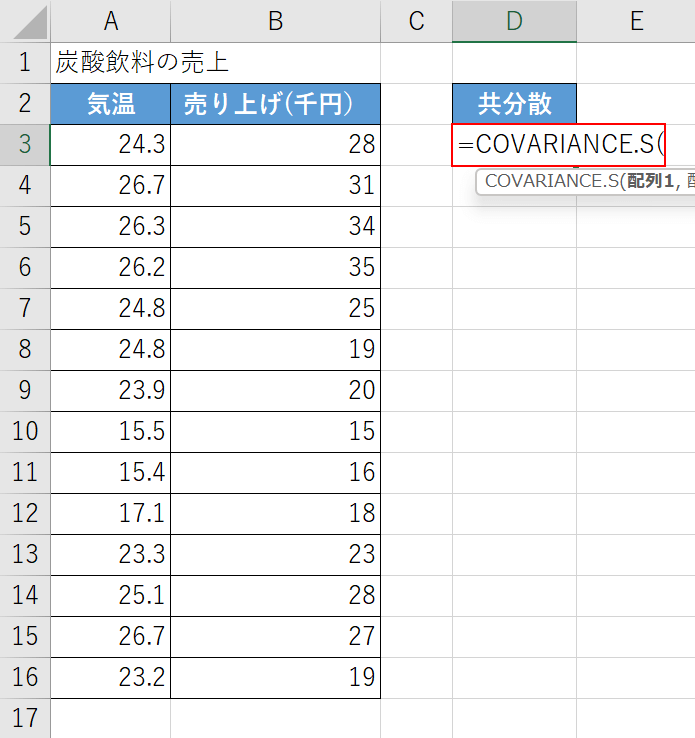
上の画像のような表を準備します。

【任意のセル（例：D3セル）】を選択し、『=COVARIANCE.S(』と入力します。

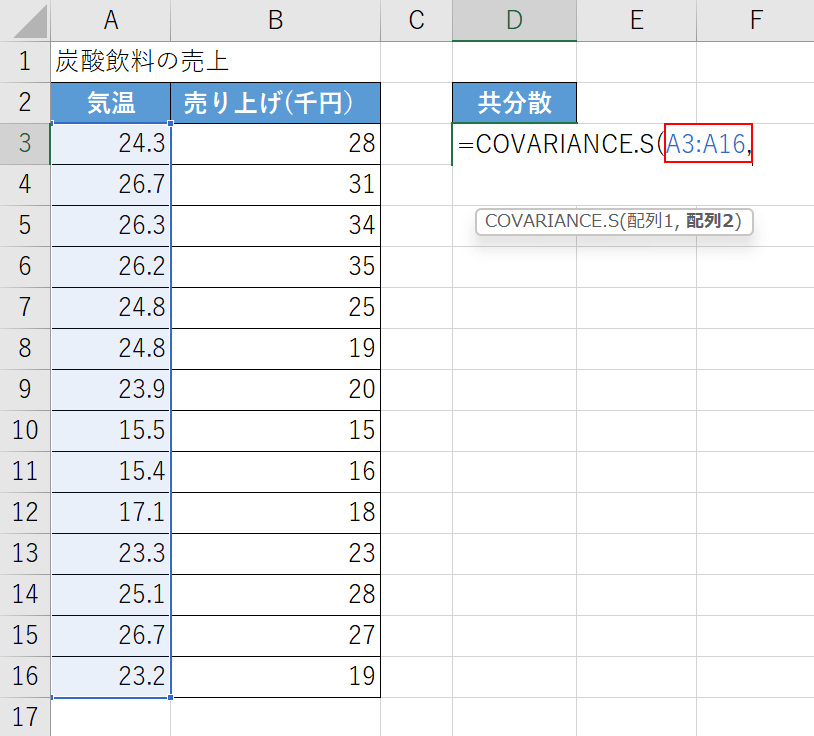
次に配列1の引数を設定します。

「気温」のリストを配列1の引数として設定します。

「=COVARIANCE.S(」に続いて『A3:A16,』と入力します。

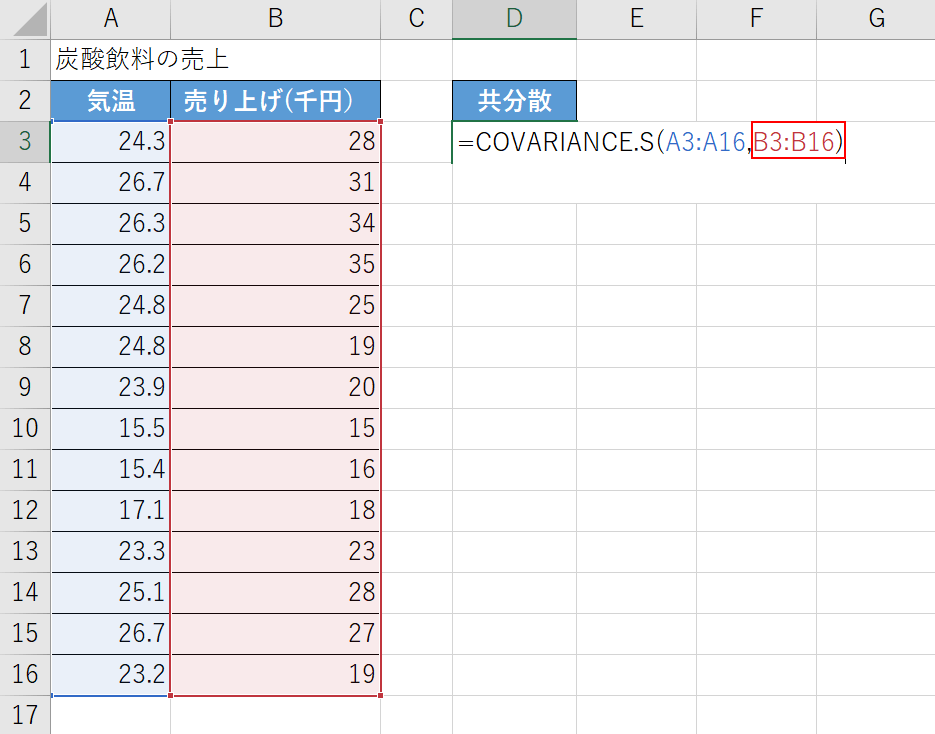
次に配列2の引数を設定します。

「売り上げ（千円）」のリストを配列2の引数として設定します。

「A3:A16,」に続いて『B3:B16)』と入力しEnterを押します。

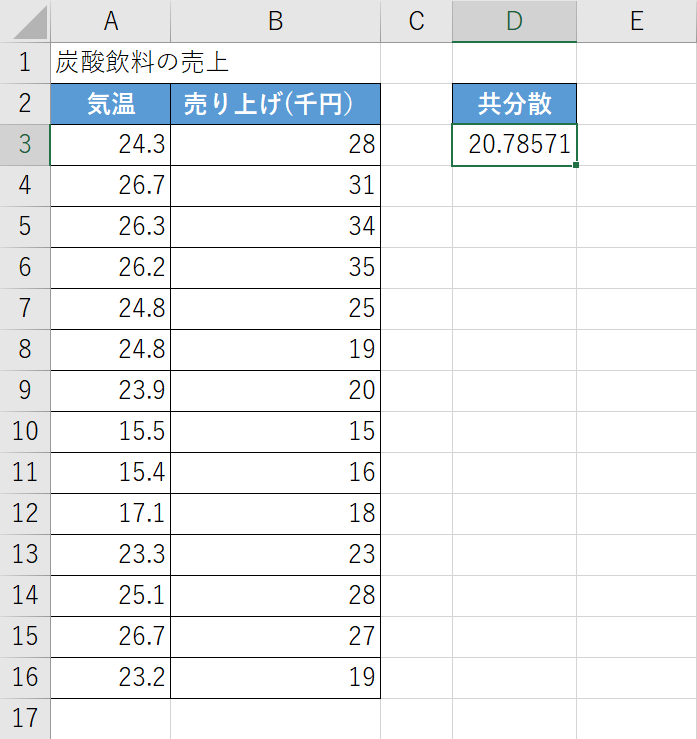
「20.78571」という結果が出ました。

0から遠い正の値であるため「気温が高いとき、炭酸飲料の売上も高い傾向がある」ことが分かります。

これでエクセルで共分散を求めることが出来ました。