エクセルで最小二乗法を計算する方法

この記事では、エクセルで最小二乗法を計算する方法についてご説明します。

最小二乗法とは、実験などで測定したばらつきのある値からデータの関係性を見出したい場合にとる手法です。

以下では、最小二乗法を求める関数や最小二乗法を使って二次方程式の傾きや切片を求める方法をご紹介します。

最小二乗法とは？

下の画像は「宣伝費と売上」について表とグラフにまとめた例です。

A列のように段階を追って宣伝費にかける金額を上げていったところ、売上がB列のように伸びていきました。

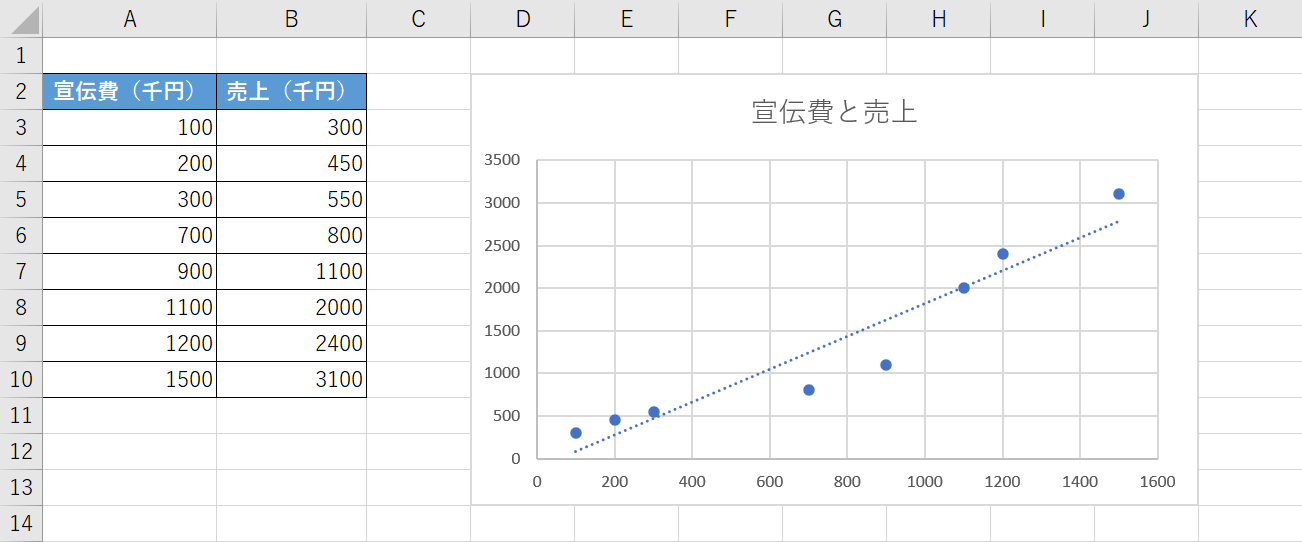
宣伝費と売上の関係には当然誤差があるため、例えば「1,000,000円かければ必ず3,000,000円の売上が上がる」とは言い切れません。

ただし、金額に差はあるものの宣伝費が上がれば売上も伸びていることが分かります。

こういった場合に、「（誤差は当然あるものとして）宣伝費を増やすと、大体どれくらい売り上げが伸びるのか」という「傾向」を見出すために使うのが最小二乗法です。

最小二乗法を使うことで、関係がありそうな2つのデータから最も確からしい直線を引くことが出来ます。

上の画像の場合はグラフ内にある右上がりの直線が、最小二乗法で求めた「宣伝費と売上がどんな関係性で伸びていくのか」という傾向を表しています。

LINEST（ラインエスティメーション）関数を使えば、簡単に最小二乗法を行うことが出来ます。

LINEST関数の書式は「=LINEST(既知のy,[既知のx],[定数],[補正])」です。

「既知のy」と「既知のx」に関係性を調べたい2つのデータを当てはめます。

「x」ではなく「y」の引数を先に入力する必要があるのでご注意ください。

最小二乗法ではいくつかの計算を行って、最終的に二次方程式を求めます。

LINEST関数を使えば、2つのデータから導き出せる直線の傾きと切片を求めることができるため、二次方程式を簡単に求めることが出来ます。

LINEST関数を使って、傾きと切片を求める方法は以下のとおりです。

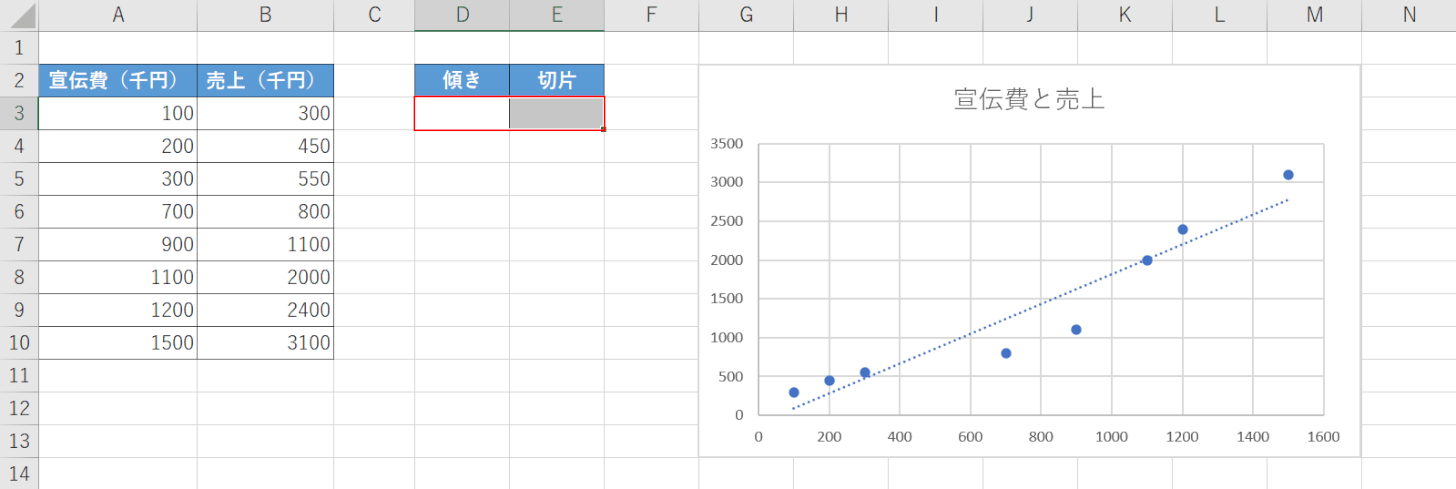
今回は、上の画像の「宣伝費と売上」の表を使ってLINEST関数で傾きと切片を求める方法をご紹介します。

LINEST関数は結果が配列で帰ってくるので、セル範囲を選択します。

【隣り合った任意のセル（例：D3セルからE3セル）】を選択します。

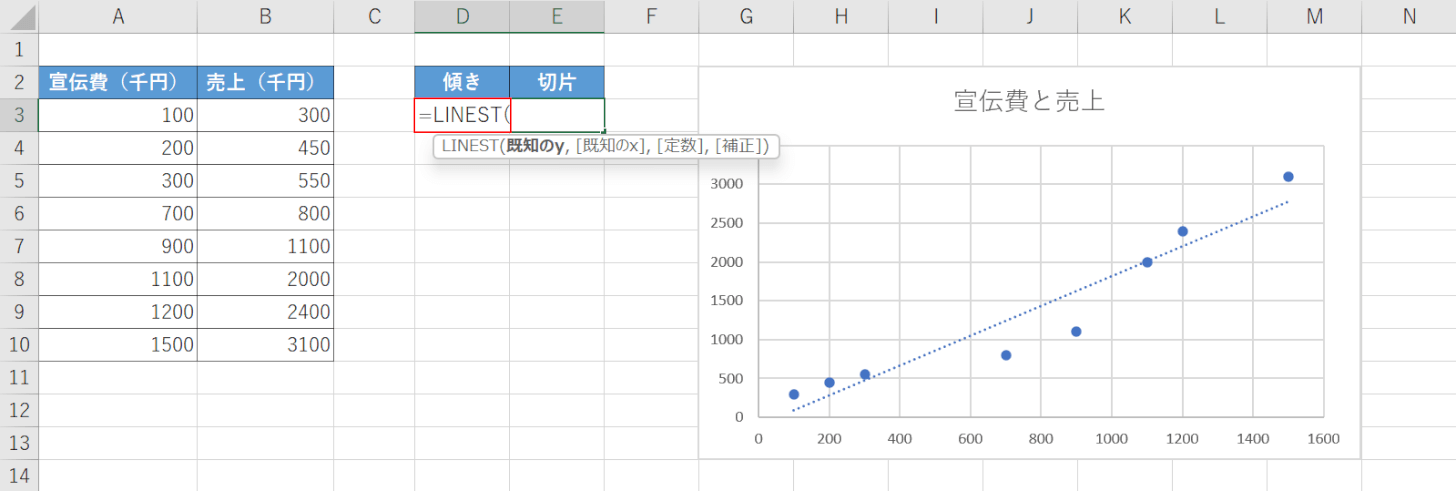
セルを選択すると、左側のセル（例：D3セル）が入力できる状態になるためそのまま関数の入力を始めます。

「隣り合った任意のセル（例：D3セルからE3セル）」を選択したまま、『=LINEST(』と入力します。

この時、改めてセルを選択し直すと正しく関数が入力できないのでご注意ください。

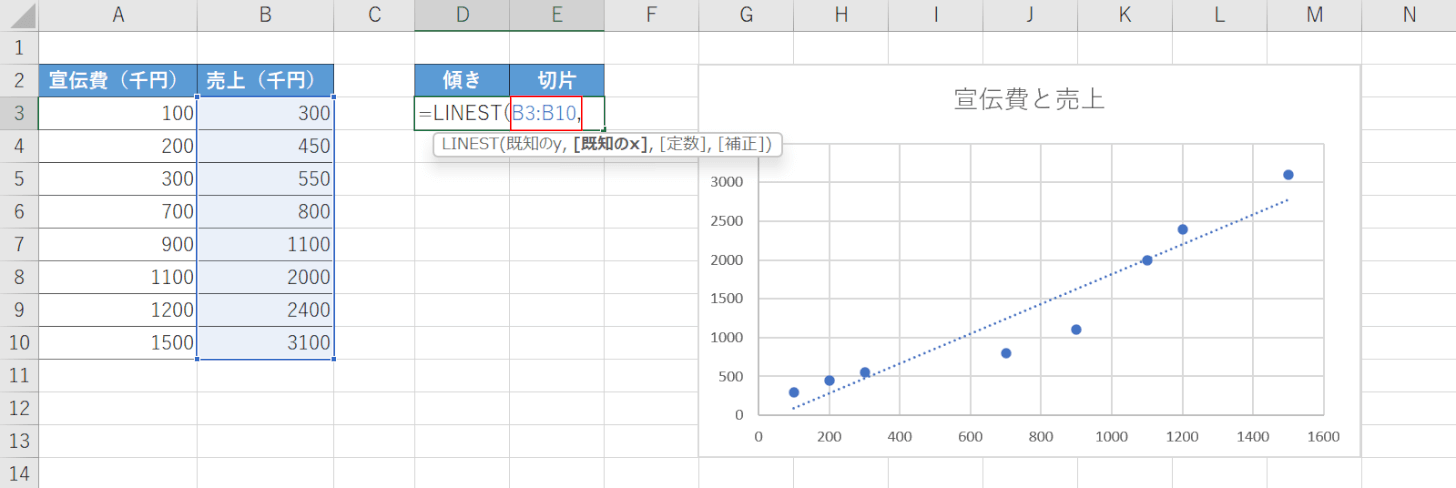
次に、既知のyの引数を入力します。

「=LINEST(」に続いて『B3:B10,』と入力します。

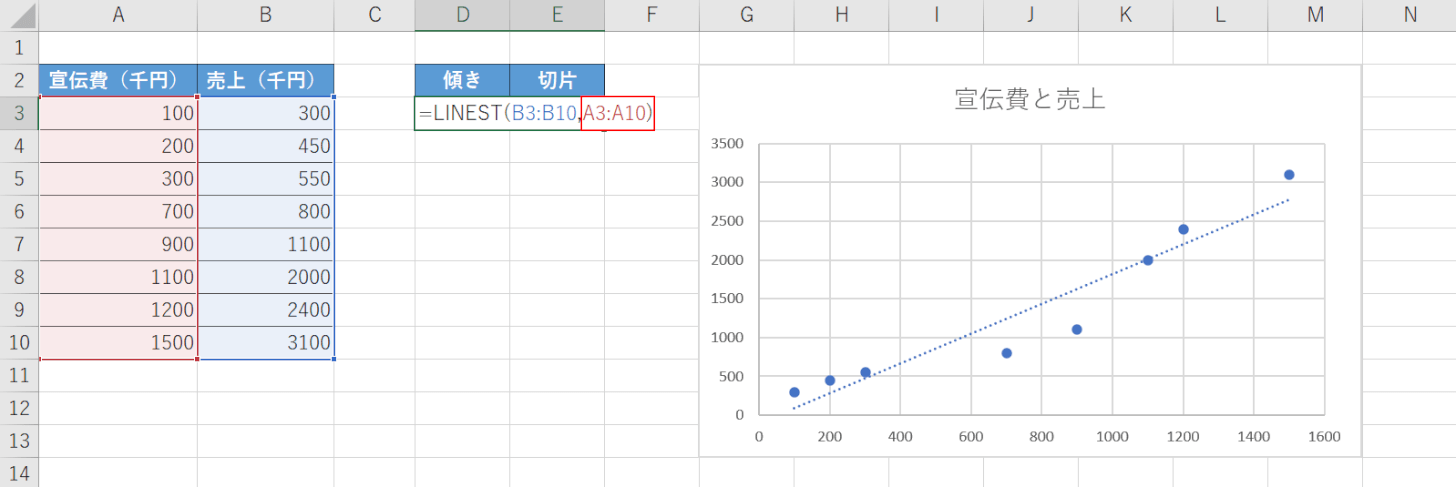
次に、既知のxの引数を入力します。

「B3:B10,」に続いて『A3:A10)』と入力し、Ctrl+Shift+Enterを押します。

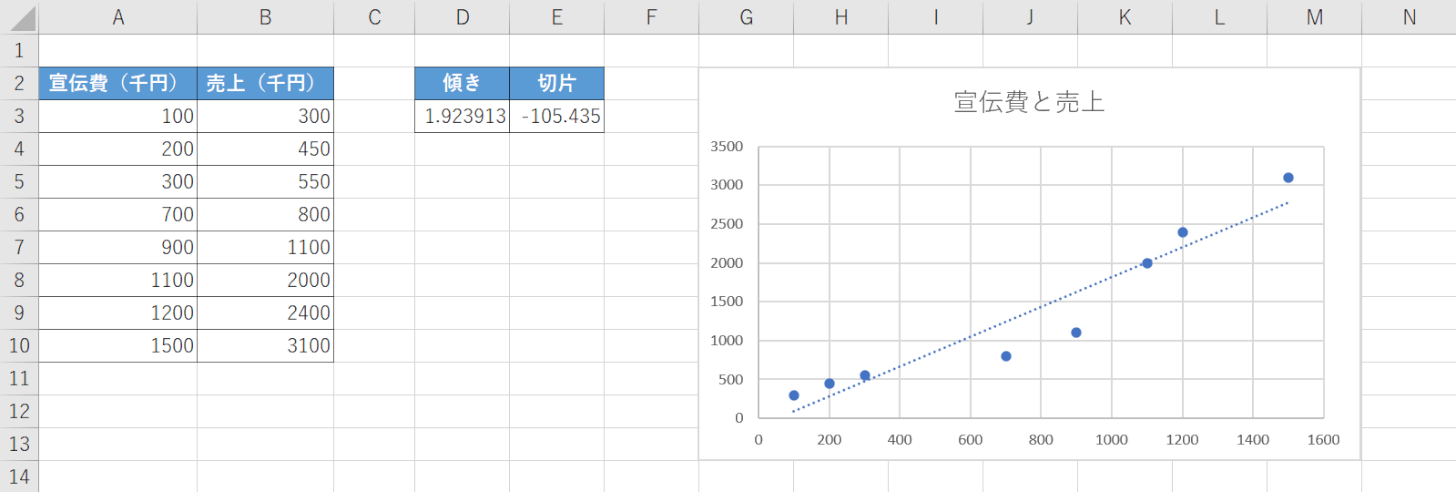
これで、LINEST関数を使って傾きと切片を求めることが出来ました。

傾きが「1.923913」、切片が「-105.435」であるので宣伝費と売上がどれくらいの関係性で伸びていくかをグラフに表すと「y=1.923913x-105.435」という二次方程式であることが分かりました。

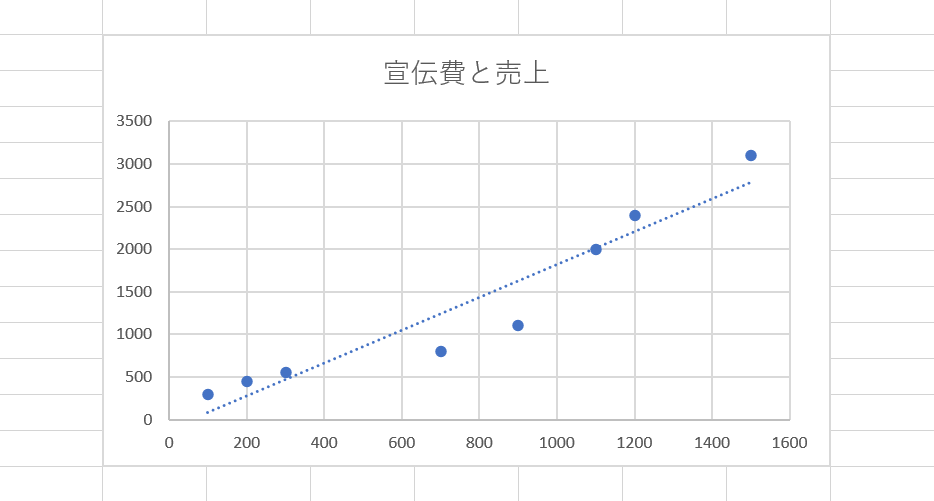
近似曲線とは、エクセルのグラフにおいてデータの推移をおおまかに表した線を指します。

近似曲線のうち、X軸とY軸に設定したデータに比例関係があると考えられる場合に使用する「線形近似」は最小二乗法で計算が行われます。

上の画像は、「宣伝費と売上」の関係において線形近似を表示した例です。

近似曲線についての詳しい情報や、基本的な使い方などについては以下の記事をご参照ください。